Question
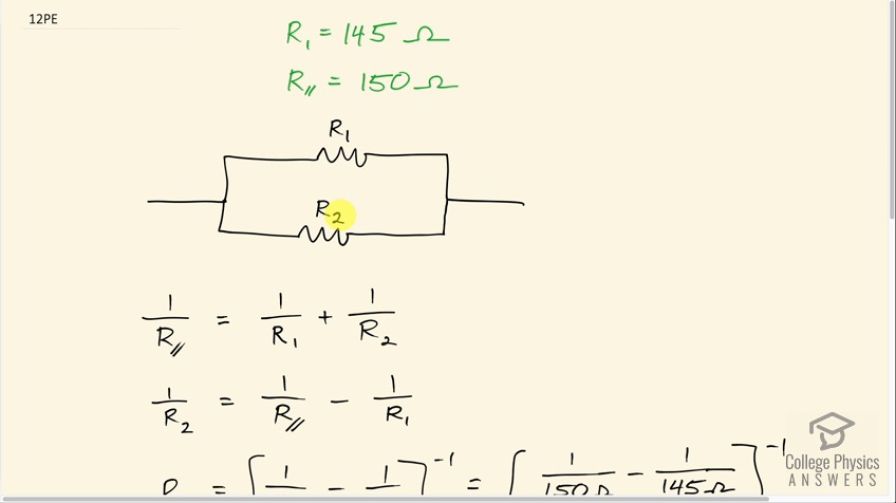
Two resistors, one having a resistance of , are connected in parallel to produce a total resistance of . (a) What is the value of the second resistance? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- A negative resistance is nonsensical
- Parallel resistance is always less than every component resistor. To say that one resistor is , and that the parallel resistance is is inconsistent with that.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 12 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question, we imagine that we have a resistor of resistance 145 ohms connected in parallel with some other resistor for a total equivalent resistance of 150 ohms and we are meant to find out what is this other resistor? So the formula for the equivalent resistance for two resistors connected in parallel is 1 over the equivalent resistance equals 1 over one of the resistors plus 1 over the other resistor and we can solve this for R 2 first by subtracting 1 over R 1 from both sides and then switch the sides around and we get 1 over < i>R 2 then is 1 over R parallel minus 1 over R 1. Then we can raise both sides to the exponent negative 1 which flips the left side solving for R 2 and on the right side, we'll just leave it as bracket 1 over R parallel minus 1 over R 1 to the power of negative 1. So we have 1 over 150 ohms minus 1 over 145 ohms all to the power of negative 1, this gives negative 4350 ohms. Now this answer is bizarre... it's nonsensical to have a negative resistance— there's no such thing— so that's our first clue that there's an issue here and parallel resistance is always less than every resistor that makes up the circuit because you know this one is a 145 ohms and giving an additional path for the current to flow is going to reduce the total resistance of this combination to something less than 145; it's impossible to have an equivalent resistance greater than any of the resistors that make up the circuit that are connected in parallel. So there we go!
