Question
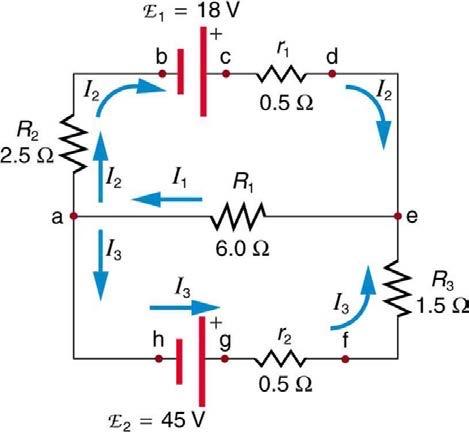
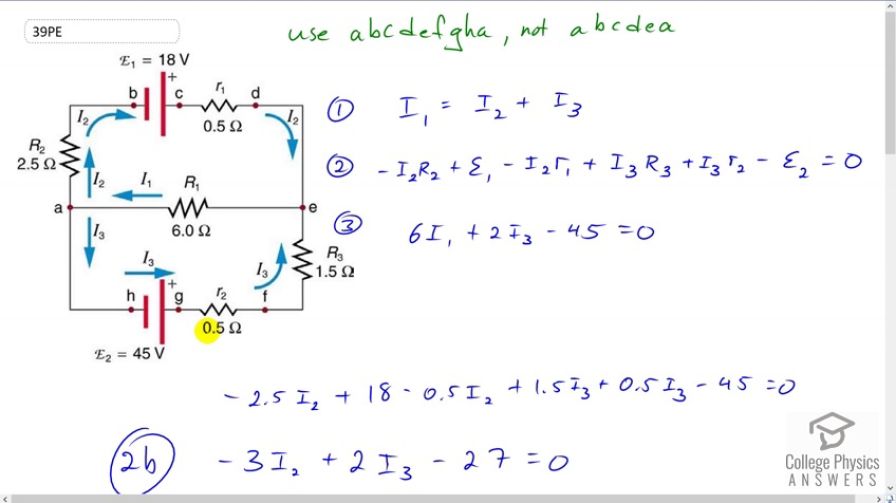
Solve Example 21.5, but use loop abcdefgha instead of loop abcdea. Explicitly show how you follow the steps in the Problem-Solving Strategies for Series and Parallel Resistors.
Final Answer
4.75 \textrm{ A}$
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us to solve this circuit using a different loop than what is chosen in the example that was given. So the example gives, this uses this loop a, b, c, d, e and back to a. And we’re told to not use that loop but instead use loop a, b, c, d, e and then f, g, h, a. So I use that and then also the loop that goes from a to e. And then down to f, g, h, and a. That would be for equation three. So we have three unknowns: I1 two and I3. And we’ll need three equations to solve for them. And so the first equation will be the Junction Rule. And we’ll take point a to be the junction. And all the currents going into it have to equal the total currents coming out. And so the currents going in are just one, I1. Then coming out we have currents I2 and I3. And then we’ll apply the Loop Rule to this outer perimeter. So we begin at point a and we traverse in this direction. And the direction of traversal is important because it affects whether potential differences are positive or negative. So when we go across resistor two, we are traversing in the direction of the current, and so this potential difference is negative. So we have a negative current two multiplied by resistance two. And then we go from negative two positive across an EMF, and so we have positive EMF one and then minus current I2 multiplied by small r1. And then here, we are traversing across resistor three in the opposite direction to the current through it. Or based opposite direction to the presumed direction of the current. When we draw these arrows for the current direction, we don’t really know what the direction is. We’re just making a guess. If we guess wrong, then our answer will be negative. That’s fine. So, across this resistor here, we traverse in the opposite direction of the current. So this is a potential difference that is positive. And so we have I3 multiplied by R3, with a plus sign there. And then we traverse this resistor on this opposite direction to the current through it so that’s plus I3 little r2. And then we go across an EMF starting at the positive, ending at the negative which is a potential drop. And so that’s negative E2. And then we return to point a. And this all equals zero. And then for this loop here, I just copied down what the example had. And they works out to six I1 plus two I3 minus 45 equals zero. And there we go. Now, we do some Algebra to solve for the unknowns. Let’s begin by considering equation two. We’re going to simplify this a little bit and collect like terms. And also substitute in the resistances. So I2 is multiplied by two and a half Ohms and so that’s a negative there. And then plus 18 Volts EMF one. And then minus 0.5 times I2 and then plus one and a half times I3. And then plus 0.5 times I3 here again. And then minus 45 equals zero, and we return to 0.8. And then collect like terms. We have an I2 term there and I2 term there. And they both have a negative coefficient. And that works out to negative three I2. And then the I3 terms. There is one there and one there, they are both positive and that makes plus two I3. And then minus 27 equals zero. Now equation three, I’m going to substitute for I1 and replace it with I2 plus I3, because then we’ll have this equation here, which has only the unknowns I2 and I3 in it. And we can combine that with equation two with also the unknowns I2 and I3. And see, when I get to this step the technique for making one of the variables disappear. So, in this equation for three, we make the substitution for I1, we’re replacing for I2 plus I3 and then, distribute this six into the bracket. And then collect like terms. And this makes a positive eight I3 and then plus six I2 there, then minus 45 equals zero. And then when you compare, equation two b with equation three b we see that, if we were to multiply equation two b by two this would become a negative six I2 and then if we add that equation, to three b, the negative six I2 from equation two would make zero combined with the positive six I2 from equation three b. And so that is the strategy and we’ll have an equation consisting of the unknown only I3. So, we have equation three b plus two times equation two b. And so I copied equation three b there. And right here. And written equation two b there with a factor of two infront of it. And then equals zero. We’re adding the equations in the right hand sides or zero in both cases. Add those together and you get zero. And on the left hand sides, add up to all this. And we multiply everything in the bracket by two. So that makes negative six I2 and positive four I3 and then negative 54. And then sure enough we have this six I2 minus six I2 making zero I2. And so I2 is no longer in this equation. And we have an equation consisting only of the one variable I3. So that’s 12 I3 minus 99 equals zero. And then take the 99 to the right hand side. And then divide by 12 you get 8.25 Amps is I3. So one of our unknown solved for. And then equation three again, return to that. And do some Algebra on this. And substitute for I3 because we know it now. And we’ll get I1. And so I took this to the right side and this to the right side, as well, by adding 45 to both sides, subtracting two I3 for both sides. And then afterwards dividing by six. And you get this line here. 45 minus two I3 all over six. So that’s 45 minus two times eight and a quarter Amps divided by six which is 4.75 Amps. Then, to find the last unknown which is I2, let’s consider the junction equation, the Junction Rule. And we’ll subtract I3 from both sides. And switch the sides around to isolate I2 on the left equals I1 minus I3. That’s four and three quarter Amps minus 8.25 Amps which is negative three and a half Amps. And the negative sign means that the current is in fact going opposite to the direction we initially guessed than it was in the drawing, which is fine. There we go.
