Question
A person with body resistance between his hands of accidentally grasps the terminals of a 20.0-kV
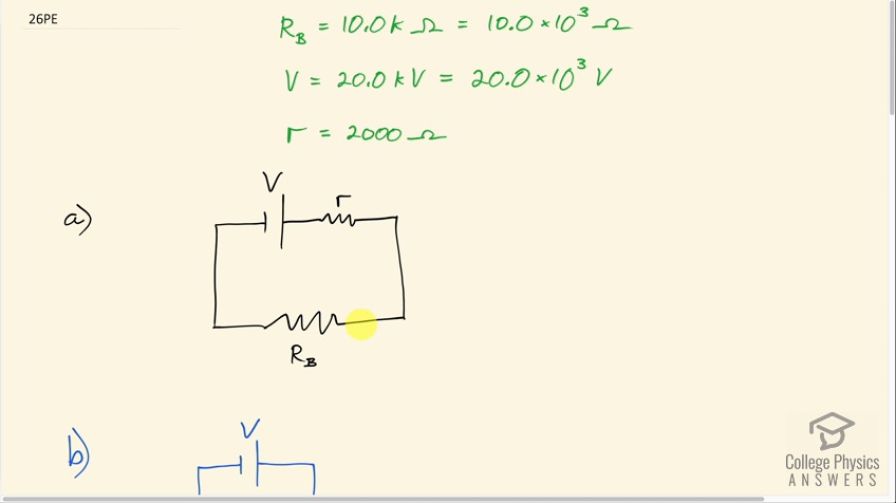
power supply. (Do NOT do this!) (a) Draw a circuit diagram to represent the situation. (b) If the internal resistance of the power supply is , what is the current through his body? (c) What is the power dissipated in his body? (d) If the power supply is to be made safe by increasing its internal resistance, what should the internal resistance be for the maximum current in this situation to be 1.00 mA or less? (e) Will this modification compromise the effectiveness of the power supply for driving low-resistance devices? Explain your reasoning.
Final Answer
- Please see the solution video
- The power supply can be effective only with low current, which is still possible with low resistance devices if the voltage is low enough. For example, with a device, the current would be only 1.00 mA if the voltage was only 2.50 V.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A person with resistance in their body between their hands of 10.0 kiloohms touches the terminals of a power supply, which has 20.0 kilovolts and the power supply has an internal resistance of 2000 ohms and part (a) asks us to draw a circuit diagram of the situation. So this would be the person's right hand and their left hand here touching the terminals of this power supply in this combination here of an emf and an internal resistance is the power supply. I have converted the units into ohms and volts so that we can use these numbers together in our equations and not have to worry about unit conversions later. So part (b) asks what is the current going through the person's body? So we redraw this circuit with a single equivalent resistance and since the internal resistance of the power supply and the resistance of the person's body are in series, the equivalent resistance will be the direct sum of those two resistances— we just add them together when they are in series. And Ohm's law says that voltage is current times resistance of the circuit and we will solve this for I by dividing both sides by this total equivalent resistance, we get that the current is V over R eq and R eq is resistance of the body plus the internal resistance of the power supply so we make that substitution here and so we have 20.0 times 10 to the 3 volts divided by 10.0 times 10 to the 3 ohms plus 2000 ohms which is 1.67 amps. The power dissipated in the person's body is the current through the body squared multiplied by the body's resistance. So that's 1.6666 amps squared times 10.0 times 10 to the 3 ohms which is 27.8 kilowatts; this is a very high amount of power and definitely lethal and this number—1.67—doesn't sound like a large current but for current going through a person's body, it's very large. So part (d), let's make this power supply safer now and suppose that its internal resistance will increase as the current drawn from it increases so it sort of has a sensor for the current, which is what how circuit breakers in a house work; they are sensors for current and the circuit breaker is labeled with the maximum current that it'll allow. In a typical North American outlet, it will be 15.0 amps. Okay! So we are gonna solve this for the internal resistance and what should it be such that the current is gonna be limited to 1.00 milliamps? So we multiply both sides by the total resistance and then we get this line here and then we distribute the current factor into the brackets here and so we have current times the body resistance plus current times the internal resistance equals the voltage and then subtract IR B from both sides and we get this line and then divide both sides by the current to solve for the internal resistance r. So that will be the voltage minus the current times the body resistance all divided by the current. So that's 20.0 times 10 to the 3 volts minus 1.00 times 10 to the minus 3 amps— this is writing one milliamp in units of amps— multiplied by 10.0 times 10 to the 3 ohms all divided by 1.00 times 10 to the minus 3 amps and that is 20.0 megaohms; this is 20.0 times 10 to the positive 6 ohms. And part (e) asks, you know, if we modify this power supply so that it has an internal resistance that goes up as current goes up, for safety reasons, can it still be effective when working with low resistance devices? And it can be so long as the voltage is low enough such that the current remains low because a power supply can be effective only when it has low current now. And so for example if you have a 500 ohm device— which is kind of low resistance— the voltage, in order to have a 1.00 milliamp limit to the current, the voltage would be that current multiplied by the total resistance which will be the 500 ohms that we are imagining here hypothetically plus the 2000 ohm—minimum internal resistance— this works out to 2.50 volts. So as long as the voltage is kept to about 2.50 volts with a small resistance device, it can still function properly.