Question
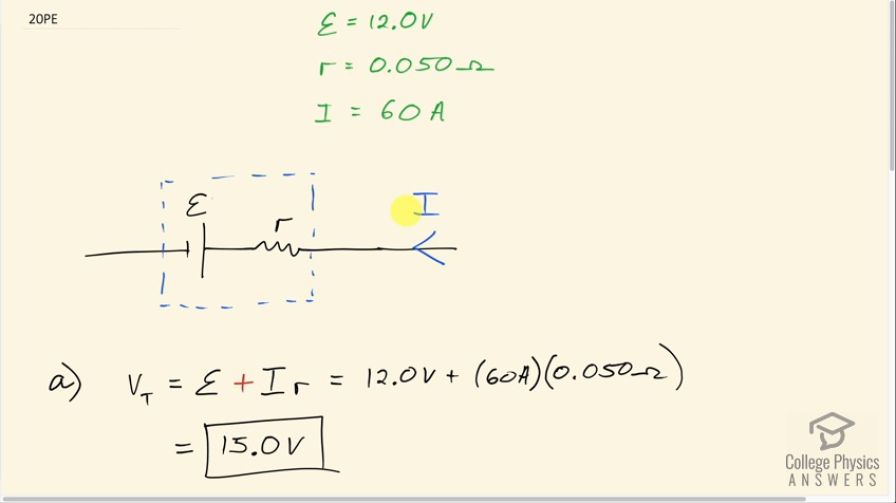
A car battery with a 12-V emf and an internal resistance of is being charged with a current of 60 A. Note that in this process the battery is being charged. (a) What is the potential difference across its terminals? (b) At what rate is thermal energy being dissipated in the battery? (c) At what rate is electric energy being converted to chemical energy? (d) What are the answers to (a) and (b) when the battery is used to supply 60 A to the starter motor?
Final Answer
- ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A battery with a 12.0 volt emf and an internal resistance of 0.050 ohms has a current of 60 amps charging it and what that means when it's charging it, the current is directed towards the positive terminal of the battery. So normally in our circuits where the battery is providing the current, the current is directed away from the positive terminal but in this case since the battery is being charged, it's going to the left and the question is what is the terminal voltage? So between here and here—these are the ends of the battery— the internal resistance is inside the battery as the emf is as well, this is the voltage we want to calculate in part (a) and we use sort of the Kirchhoff's loop rule way of looking at things. So we are gonna traverse this section of some circuit... I mean we haven't got the rest of it drawn and that's fine but we are gonna traverse it in this direction to the right and we start at the negative terminal and end at the positive terminal of this emf and that's a gain in potential and then we are traversing this resistor in the opposite direction to the current through that resistor and so what that means is this will be a positive change in potential as we go from left to right given that the current is going from right to left and so that's where this plus sign comes from here in our terminal voltage formula, which is normally written as emf minus current times internal resistance and that's the case for the situation where the battery is providing the current but in this case where they are being charged, we have a plus sign there. So we have 12.0 volts of the emf plus 60 amps times 0.050 ohms and that's 15.0 volts is the terminal voltage. And part (b) asks at what rate is thermal energy being dissipated in the battery? Well it's being dissipated in the internal resistance. So we multiply that by the square of the current going through that resistance. So 60 amps squared times 0.050 ohms which is 180 watts. In part (c), we are asked at what rate is electrical energy being converted into chemical energy, which is the whole point of this charging business is to take some electrical energy provided by the wall socket say into electro-chemical energy stored in the battery. So the total power that's being used or the total rate at which energy is being converted into some other form instead of electrical energy, it's being converted into both thermal energy in the resistor— as we calculated in part (b)— and also being converted into electro-chemical energy that's being stored in battery. So this total is going to be the current through the battery multiplied by the terminal voltage— that we just calculated in part (a)— and this total we can also think of as the sum of the energy rate of energy conversion into electro-chemical energy and the rate of thermal energy production in the resistor so our job is to solve for this P ε. So we'll subtract the rate of thermal energy production P r from both sides— this T does not stand for 'thermal', it stands for 'total'— and then we switch the sides around and we get the rate of electro-chemical energy storage is the total minus the rate of thermal energy production. So that's current times terminal voltage times the P r that we calculated before and this is 60 amps times 15.0 volts minus 180 watts which is 720 watts. And part (d) asks what are the answers to parts (a) and (b) when the battery is used to supply 60 amps to the starter motor? So that means the circuit is now the same as before except that... let's copy this down here... except that the current is now going to the right because the battery is providing the current now instead of being charged as it was before. And so what that means is if we traverse this section from left to right, we have a positive change in potential across the emf—as we did before— but now we are traversing this resistor in the same direction as the current through it and so that means that we will have a drop in potential and that's why there's a minus sign here. So the terminal voltage now is 12.0 volts minus 60 amps times 0.050 ohms and that is 9.00 volts and the rate at which energy is converted into thermal energy in the resistor is the 60 amps squared times 0.050 ohms of the resistor which is 180 watts. It's the same rate of thermal energy production as it was when the battery was charging because the current through the resistor is still the same.

