Question
A resistor, an uncharged capacitor, and a 6.16-V emf are connected in series. (a) What is the initial current? (b) What is the RC time constant? (c) What is
the current after one time constant? (d) What is the voltage on the capacitor after one time constant?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 68 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
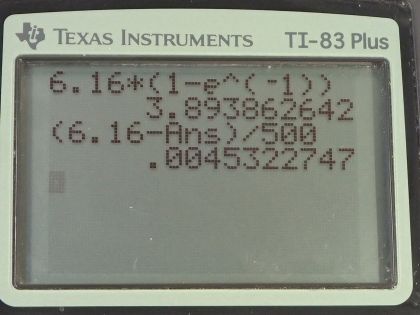
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An emf, a resistor and capacitor are connected in series and the first question is what is the initial current? Well we use the Kirchhoff's Loop rule starting from here ending here say and when we traverse this emf, that's a positive change in voltage and then minus the current times resistance and we will assume current is going this way away from the positive terminal of the emf and then minus the voltage across this capacitor and all that equals zero. Well the voltage across the capacitor is the charging emf times 1 minus e to the negative t over resistance times capacitance but t is zero initially so this e to the 0 is 1. and then we have emf times 1 minus 1 equals 0 so in other words, the voltage across the capacitor initially is zero and we could have probably said that through intuition without using these equations that it should be uncharged initially but question even says that actually but anyway here is a more fancy way of saying it's uncharged. Okay! So we have zero for V C and we can solve for I and we'll add IR to both sides and then divide both sides by R afterwards and we get the current then is the emf divided by the resistance 6.16 volts divided by 500 ohms is 12.3 milliamps. The time constant is the product of resistance and capacitance; 500 ohms times 1.50 times 10 to the minus 6 farads gives us 7.50 times 10 to the minus 4 seconds. What is the current after one time constant? So we need to figure out what is the voltage across a capacitor after one time constant which means by the way that t equals the time constant τ, which is RC. So we have the voltage across a capacitor is the emf times 1 minus e to the negative RC in place of t divided by RC and so that's emf times 1 minus e to the negative 1 and this works out to 6.16 volts times 1 minus e to the negative 1 which is 3.89386 volts. So we return to this work that we did in part (a) and now we have a number for V C that's not zero and we'll add IR to both sides and switch the sides around and we have IR equals ε minus V C then divide both sides by R and we get the current then is emf minus voltage across a capacitor divided by resistance 6.16 volts minus 3.89386 volts divided by 500 ohms is 4.53 milliamps. Part (d) what is the voltage on the capacitor after one time constant? Well, we had to figure that out in order to answer part (c), it is 3.89 volts.