Question
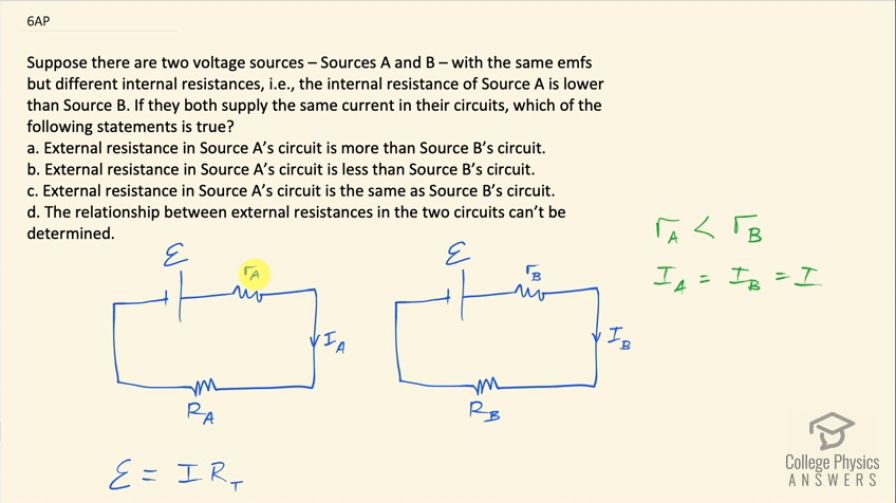
Suppose there are two voltage sources – Sources A and B – with the same emfs but different internal resistances, i.e., the internal resistance of Source A is lower than Source B. If they both supply the same current in their circuits, which of the following statements is true?
- External resistance in Source A’s circuit is more than Source B’s circuit.
- External resistance in Source A’s circuit is less than Source B’s circuit.
- External resistance in Source A’s circuit is the same as Source B’s circuit.
- The relationship between external resistances in the two circuits can’t be determined.
Final Answer
(a)
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 6 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two different circuits one is with a battery that has an internal resistance r A and an external resistance we'll call R A and some current I A and an emf... the emf in both these cases does not need a subscript because they have the same emf we are told. We can also get rid of the subscript on the currents here because we are told that the currents are the same... the same current so let's just call it I and we have to create a relation between the external resistances here knowing that the internal resistance of the battery in case B is greater than the internal resistance in scenario A or you could say internal restistance A is less than internal resistance B. Okay! So knowing all this what can we say about the external resistances? Well we know that the total emf is the current through the circuit multiplied by the total resistance and we can solve for current by dividing both sides by R T and so the current then is emf divided by r A plus R A and likewise we can say that same current because we are told the currents are the same in both cases, the current in scenario B is the same emf divided by internal resistance B plus external resistance B and we can equate these two things because they are both equal to the same current and we can multiply both sides by r A plus R A and then also multiply both sides by internal resistance B plus external resistance B these are multiplied here and then divide both sides by emf and the emf is a common factor that's going to cancel here and we end up with this line here and this can be rearranged to say R A minus R B and that is R A minus R B which we get by subtracting R B from both sides and then also subtract r A from both sides and switch the sides around you get this relation, which says that R A minus R B equals r B minus r A. So this is saying the external resistance in circuit A minus the external resistance in circuit B equals the internal resistance of battery B minus the internal resistance of battery A and we know this is greater than zero since we are told that r B is more than r A, which means, you know, we have R A minus R B is greater than 0, in which case you can add R B to both sides and you get this conclusion here which is that the external resistance in circuit A is greater than the external resistance in circuit B so the answer is (a).