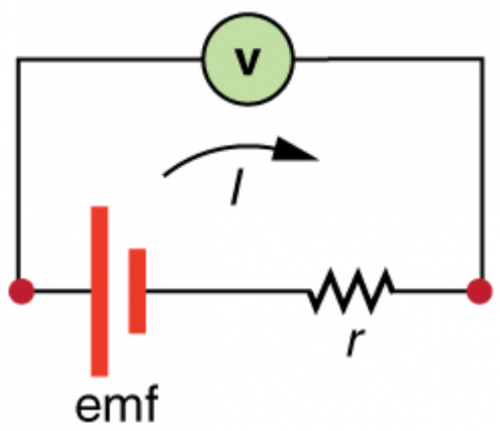
Question
Suppose you measure the terminal voltage of a 1.585-V alkaline cell having an internal resistance of by placing a voltmeter across its terminals. (See
Figure 21.54.) (a) What current flows? (b) Find the terminal voltage. (c) To see how close the measured terminal voltage is to the emf, calculate their ratio.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 50 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
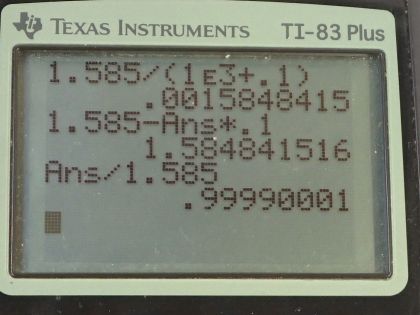
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a battery with an internal resistance r of 0.100 ohms, an emf of 1.585 volts and a voltmeter with a resistance of 1.00 kiloohm, which is 1.00 times 10 to the 3 ohms. This is the whole circuit and our question is how much current is flowing in this circuit? And the emf is going to be the current multiplied by the equivalent resistance of the circuit, the total resistance in other words— this is Ohm's law— and this total resistance is the resistance of the voltmeter plus the resistance of the battery its internal resistance. So this gets substituted in place of R eq and we do that here. Then we solve for I by dividing both sides by the total resistance and we get the current then is the emf divided by the total resistance. So that's 1.585 volts divided by 1.00 kiloohm plus 0.100 ohms and that's 1.58 milliamps. And we expect the current to be really low because... when designing a voltmeter, you want it to be such that it causes as little current through it as possible because this current through it actually changes this voltage that it's measuring it's sort of like the act of measuring changes the thing being measured to some extent so... yeah, reducing the current through the voltmeter by increasing the resistance of the voltmeter minimizes that effect. Okay part (b) terminal voltage is going to be the emf minus the current multiplied by the internal resistance so this is the voltage drop across the internal resistance. So that's 1.585 volts minus this current multiplied by 0.100 ohms and it still works out to 1.585 volts when you have four significant figures. And in part (c) we are meant to find this terminal voltage as a ratio of the emf so we take that answer for part (b), divide it by 1.585 volts emf and that's 0.9999. So the terminal voltage is nearly the same as the emf.