Question
Find the resistance that must be placed in parallel with a galvanometer having a sensitivity (the same as the one discussed in the text) to allow it to be used as an ammeter with a 10.0-A full-scale reading. Include a circuit diagram with your solution.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
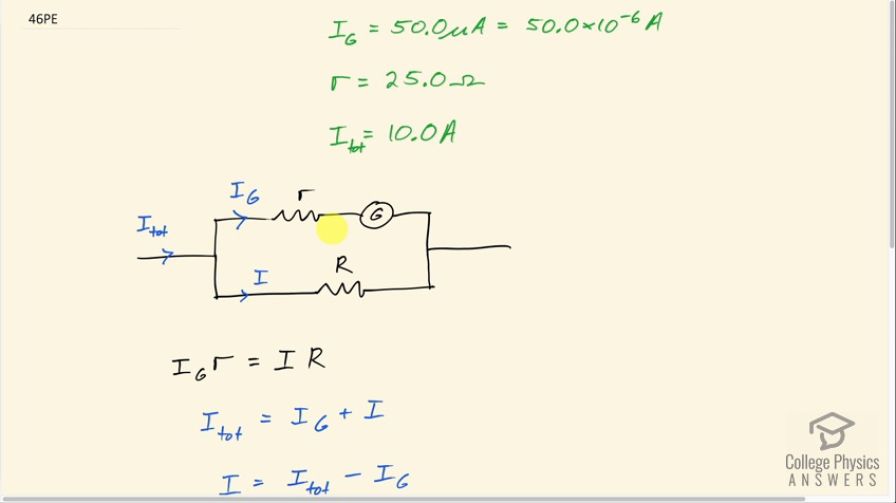
This is College Physics Answers with Shaun Dychko. We have a galvanometer that has an internal resistance of 25.0 ohms which we have labeled r and it will be in parallel with some other resistance R— this is called the shunt resistance— and it's meant to be really small such that this current basically travels through this ammeter thing without being impeded too much. So this shunt resistance is kept really low so that the current has a place to flow unrestricted because we don't want the ammeter to be changing the current in the circuit, it's one of these instances where the act of measuring something such as a current is actually changing the thing being measured and we want to minimize that effect by having a really small shunt resistance. Okay! So we are told that the sensitivity of the galvanometer is 50.0 microamps so that means its maximum reading will occur when this I G—for galvanometer current— is 50.0 microamps so we know that current in this branch and then the total current is meant to be 10.0 amps when the current through the galvanometer is 50.0 microamps. So what is this shunt resistance is the question? Now the voltage between here and here has to be the same as the voltage between here and here because these two branches are in parallel and the voltage across the top part is the current through the galvanometer multiplied by its internal resistance r and that's gonna equal the current through the shunt resistor multiplied by the shunt resistance. Now the total current going into these two branches has to equal the total current coming out of that junction, this is one of Kirchhoff's rules, the Junction Rule— total current going in has to equal total current going out— and then we will rearrange this to solve for I by just subtracting I G from both sides and now we have the current through the shunt resistor is the total current that we know minus the galvanometer current which we also know. So we substitute those in place of I and then solve for the shunt resistance by dividing both sides by this I total minus I galvanometer and then switch the sides around and we get then the shunt resistance is 50.0 microamps times 25.0 ohms divided by 10.0 amps minus 50.0 microamps and that is 1.25 times 10 to the minus 4 ohms and we get a really small answer here for our resistance in the shunt resistor and that is what we expect so that's good.
