Question
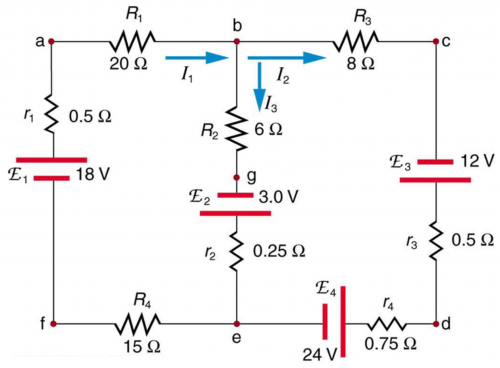
Find the currents flowing in the circuit in Figure 21.47.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
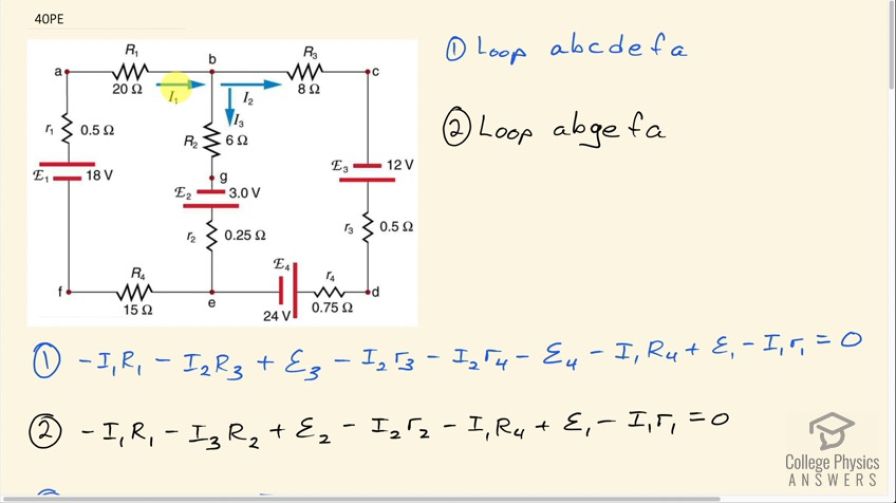
Video Transcript
This is College Physics Answers with Shaun Dychko. This is figure [21.47] and we are going to figure out what all of the currents are; there are three of them: I 1, I 2 and I 3 and we have some resistances given to us and some emf's and we are going to figure out these currents using Kirchhoff's rules. So we have two rules to think about: one is the Loop rule which says that in a loop, the total changes in potential have to add up to zero and then we have the junction rule which says all the currents going into a point have to equal all the currents coming out of that point. Okay! So we are going to use two loops and one junction rule. So the first loop we will think about is starting at point a going to b and then c, d, e, f and then back to a so that's the outside perimeter of a circuit. Then the second loop, we'll go a, b and then cut down the middle to g and then e, f and then back to a. So we will write down expressions for all the different changes in potential as we go through the loop and then as a next step, I will substitute in numbers for the resistances that we are given. Okay! So starting from here, we are going to be traversing this loop in yellow we are going to be traversing in this direction which is in the same direction as this current I 1 so that means that going across this resistor is a drop in potential so that's why we have a negative sign I 1 multiplied by capital R 1. Then we will continue to traverse resistor R 3 and we are going in the same direction as the current through it so there's another drop in potential so minus I 2 times R 3 and then we go from the negative terminal and then end on the positive terminal of an emf and so this is negative and this is positive because this is longer so we end up at a higher potential here so this is an increase in potential so that's plus ε 3 and then minus current I 2 which is going down here through resistor r 3 so we multiply I 2 by r 3 and that's a minus there and then minus I 2 times r 4 as we traverse to the left here and then we are starting at the positive plate of this emf and ending at the negative plate and so this is a drop in potential and so that's why we have a minus ε 4 there and then we are back into this section here which has a current I 1 again because if this is I 1 up here then it has to have the same current in that whole up to the next junction like between junctions, the current is going to be the same along a single branch. So this is current I 1 down here to the left and we are traversing to the left and so this is a drop in potential as we traverse R 4 and so we have a minus I 1 times R 4 there and then we go up through this emf starting at the negative plate ending at the positive so we are increasing potential ε 1 and then minus I 1 times r 1 and finally, we return to where we started and then we say everything equals zero because this is conservation of energy— the total change of potential in any closed loop has to be zero. Okay! Then we have the loop abgefa so we start in the same position again and we are going to traverse R 1 the same as we did before so it's minus I 1 times R 1 but now it's minus I 3 times R 2 as we cut down the middle here so we are traversing in the same direction as the current I 3 through this resistor R 2 so we have minus I 3 times R 2 and then plus this change of potential here since we start at the negative terminal and end at the positive terminal of this emf and so we have plus ε 2 and then minus I 2 times r 2 and then we go to the left here and it's minus I 1R 4 plus ε 1 minus I 1r 1 in the same way as we did before as we go through this section here again... okay and then all that equals zero. So third equation says that the total currents going into this junction at b, which is I 1, equal the total currents coming out which is I 2 plus I 3 and so we have a simple equation there for the junction rule. Then as a next step, we'll take this equation one and substitute in the resistances and so we have minus 20I 1 minus 8I 2 plus 12 minus 0.5I 2 minus 0.75I 2 minus 24 volts there minus 15 times I 1 plus 18 minus 0.5 times I 1 all of that equals zero and now we will collect like terms. So we have the minus 20I 1 and the minus 15I 1 and the minus 0.5I 1 all those combine to make minus 35.5I 1. Then we have the I 2 terms there's one there and there's one there and one there and all those combine to make negative 9.25I 2 and then plus the constant term which is 12 minus 24 plus 18 which is plus 6 and all that equals zero. So we'll call it equation one... I called it equation one before but here is the equation we will be working with with some numbers substituted for the resistances. And then equation two, it's the same story but just with different numbers in some cases so we plug in the resistances again so it's minus 20I 1 the same as before but now it's minus 6 times I 3 and then plus 3 volts here minus 0.25 times I 3 minus 15I 1 plus 18 minus 0.5I 1 as we go through this branch here again and then combine the like terms so we have an I 1 term and an I 1 term and an I 1 term so that's minus 35.5I 1 again and then the I 3 terms are here and here that makes minus 6.25I 3 and then the constant terms plus 21 and all that equals zero. So we have three equations that we can work with here: we have equation one, two and three. And the physics is done now; the physics of this question was how to make the equations so this is a conservation of charge concept and this loop rule comes from conservation of energy but from this point on, it's now a math question how to solve this system of three simultaneous equations and there are two main things you can do: one is you can substitute from one equation into the other and replace one of the variables to get rid of it and put the other variables in its place and the other strategy is to add equations together to make a variable disappear and we are gonna do both those things. So first of all, I am gonna substitute equation three into equation one so equation three says I 1 is I 2 plus I 3 so wherever I see I 1 in equation one, I can write it instead as I 2 plus i 3 so that's what I have done in red here. So this is equation one rewritten with I 2 plus I 3 substituted for I 1. So then multiply through into the brackets here and we have minus 35.5I 2 minus 35.5I 3 minus 9.25I 2 plus 6 equals 0, collect these like terms and we have minus 44.75I 2 minus 35.5I 3 plus 6 equals 0 and this is useful because we have removed the variable I 1 from this equation and we can do the same in equation two and then we'll have two equations with only two unknowns and so that gets us closer to finally solving for one of those unknowns. So we are gonna do the same trick with equation two and replace I 1 with I 2 plus I 3 in that equation. So it's minus 35.5 times I 2 plus I 3 and distributing into the brackets there gives us this and then minus 6.25I 3 plus 21— because that's what we have from equation two— all equals zero and then combine these like terms here and we have minus 35.5I 2 minus 41.75I 3 plus 21 equals zero. So now we have equation 1b and equation 2b that's two equations with two unknowns so we are one step closer to solving this question. So how do we combine these to get rid of one of the variables to solve for the other? So what I am going to do is multiply equation 2b by this fraction that is strategically chosen so that the coefficient for the I 2 term becomes the same as the coefficient of the I 2 term in equation 1b. So if you multiply 35.5 by 44.75 divided by 35.5 then the 35.5 factors will cancel leaving us with 44.75, which is the same as the coefficient for I 2 in equation 1b and then we will subtract the equations or I like to think of it as adding the negative of equation 1b so that the coefficient of I 2 will be the same but the opposite sign and then it will add up to zero and then I 2 will disappear. Okay! So equation 2b is getting multiplied by this fraction both sides but I guess it's trivial to say that though because on the right hand side, it's a zero and so whatever this thing is multiplied by zero still makes zero on the right side but you know, it's just good to keep that in mind because sometimes if it's not zero, you would have to multiply whatever it is by this fraction as well. Alright so... multiply all of this by this fraction. Multiplying the I 2 part is straightforward it becomes negative 44.75 times I 2 and then we also have to multiply this term by it as well so we have minus 44.75 over 35.5 times 41.75 all times I 3 and we will need our calculator to figure out what that is plus 44.75 over 35.5 times 21 and then we add the opposite of 1b and by opposite, I mean change the signs of every term. So we are gonna add positive 44.75I 2 plus 35.5I 3 minus 6 and that's what I have written here and all this equals zero because we are also adding the right hand sides, which in both cases is zero. So now we combine... well, we'll figure out what these coefficients are the I 2 terms are gone— they added up to zero—this is positive 44.75I 2 and this is negative 44.75I 2 so that makes zero and then this term becomes minus 52.6285I 3 plus 26.47183 plus 35.5I 3 minus 6 and then combine the like terms and we have minus 17.1285I 3 plus 20.47183 equals 0 and then we have I 3 after we subtract 20.47183 from both sides and divide both sides by this coefficient of I 3, which is negative 17.1285 and we get our answer: 1.20 amps. So great! We have one of our three currents solved for and I kept the unrounded number here that we'll use in subsequent work for solving the other currents. Let's return to equation two and originally it's up here and I copied it here and we are going to solve this for I 1 and then substitute in this known I 3 and then figure out what I 1 is. So to solve for I 1, we will first isolate it on the left hand side by adding 6.25I 3 and minus 21 from both sides plus 6.25I 3 and then minus 21 from both sides and we have negative 35.5I 1 equals negative 21 plus 6.25 I 3 and then divide both sides by negative 35.5 and I don't know why but I just felt like... switching the signs of the terms in the top around and then making the bottom positive; in other words, I am multiplying top and bottom by negative 1 which is fine because you know we can multiply this negative 1 divided by negative 1 is 1 and you can multiply anything you like by 1 if you feel like it and what it does is it makes the bottom positive and it makes the top positive 21 and a negative 6.25I 3. Okay! So we have I 1 equals all this, substitute in our answer for I 3 and we end up with 0.381 amps is I 1. Then I 2 is the remaining thing we don't know and it has a nice simple junction equation to figure it out. So we'll subtract I 3 from both sides and so I 2 is I 1 minus I 3 and we have 0.38113 amps minus 1.19519 amps which is negative 0.814 amps and give yourself a pat on the back if you made it all the way through this solution and good job!


