Question
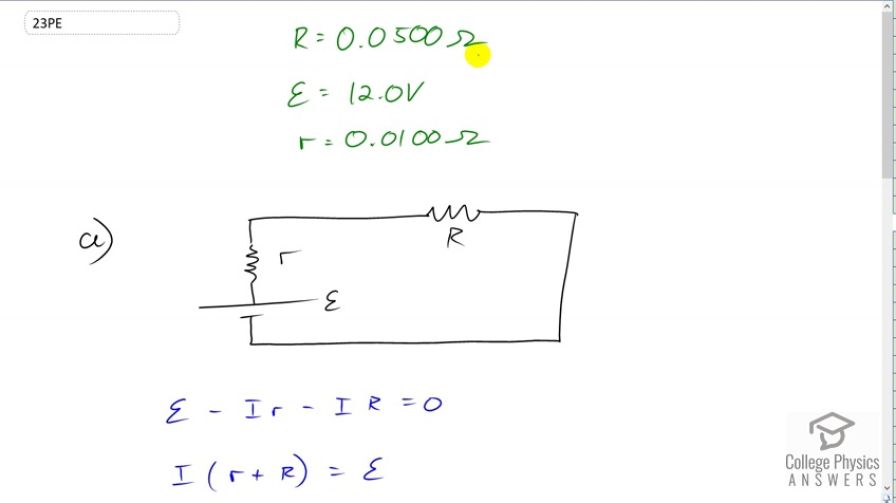
An automobile starter motor has an equivalent resistance of and is supplied by a 12.0-V battery with a internal resistance. (a) What is the current to the motor? (b) What voltage is applied to it? (c) What power is supplied to the motor? (d) Repeat these calculations for when the battery connections are corroded and add to the circuit. (Significant problems are caused by even small amounts of unwanted resistance in low-voltage, high-current applications.)
Final Answer
- , ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a battery with an internal resistance supplying an automobile starter motor with resistance capital R. The starter motor has a resistance of 0.05 ohms, the EMF of the battery is 12 volts, and the battery has an internal resistance of 0.01 ohms. So the question is what is the current going through the starter? So using the loop rule, we have that this positive EMF -- traversing the loop in this direction by the way -- there is a positive EMF minus the potential drop across the internal resistance of current multiplied by little r, and then minus the potential difference across the starter which is the same current multiplied by capital R, all that equals zero. We can add I little r and I capital R to both sides and then factor out the capital I, and we have capital I times little r plus capital R, all equals EMF. Then divide by this total resistance, both sides. So the current is EMF over little r plus capital R. So that's 12 volts minus 0.01 ohms plus 0.05 ohms giving us 200 amps is the current. Then the voltage across the starter or the load, is the current multiplied by its resistance. So that's 200 amps times 0.05 ohms which is 10.0 volts. The power dissipated by the starter will be the current through it squared multiplied by its resistance. So that's 200 amps squared times 0.05 ohms which is 2.00 kilowatts. In part D, we're asked to do this calculations again but assuming we have an additional 0.09 ohms of resistance due to corrosion of the wires connecting the battery to the starter. So the total internal resistance you could say the resistance, the internal resistance of the battery plus you know, the wires, this all adds up to 0.100 ohms. So we do these calculations again with 0.1 in place of little r. So we have the current through the starter is 12 volts divided by 0.1 plus 0.05 which is 80 amps. The voltage across the starter will be 80 amps times 0.05 ohms which is 4.00 volts and that's a lot less than the 10 volts that we had before. Therefore the power dissipated by the load is also going to be a lot less. 80 amps squared times 0.05 ohms giving 320 watts. So this shows that in circuits that have low voltage and high current, that a small additional resistance has a big effect on the circuit.

