Question
You are pumping up a bicycle tire with a hand pump, the piston of which has a 2.00-cm radius. (a) What force in newtons must you exert to create a pressure of (b) What is unreasonable about this (a) result? (c) Which premises are unreasonable or inconsistent?
Final Answer
- The force requires all the weight of an 88 kg person. This is not reasonable.
- The radius of the pump cylinder is too large.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 85 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
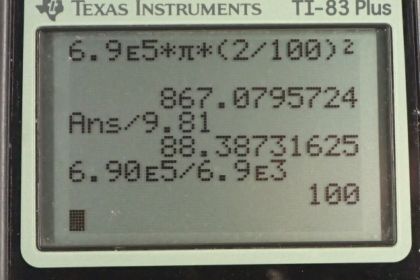
This is College Physics Answers with Shaun Dychko. We're going to calculate the force needed to operate this bicycle pump by saying that pressure is force divided by area and then multiplying both sides by a to solve for F, the force. So force is pressure times area and that's pressure times pi r squared, area of a circular piston. That is 6.9 times ten to the five Pascals times pi times two centimeters converted into meters by multiplying by one meter for every 100 centimeters, and then we square that result, and we get 867 newtons. This force is too high, it's not reasonable because if somebody put all of their weight on the handle of the pump, this would require somebody who had a mass of 88 kilograms to operate the pump, like standing on it basically and that's not reasonable to expect somebody to be this massive and stand on the pump. So the problem here is that the radius of the pump is too large and so you'll never find a hand pump which is that big. So the pressure of this converted into psi is 100 psi and that's maybe a bit high but maybe for competitive road cyclists, they might have pressures that are that high in the tires. So it's somewhat reasonable but the radius is the part that's not reasonable.