Question
(a) The pressure inside an alveolus with a 2.00×10−4 m2.00 \times 10^{-4} \textrm{ m} radius is 1.40×103 Pa1.40 \times 10^3 \textrm{ Pa}, due to its fluid-lined walls. Assuming the alveolus acts like a spherical bubble, what is the surface tension of the fluid? (b) Identify the likely fluid. (You may need to extrapolate between values in Table 11.3.)
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 0.0700 N/m0.0700 \textrm{ N/m}
  2. This fluid is probably water at 37∘C37^\circ \textrm{C}

Solution video

OpenStax College Physics for AP® Courses, Chapter 11, Problem 55 (Problems & Exercises)

OpenStax College Physics, Chapter 11, Problem 55 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

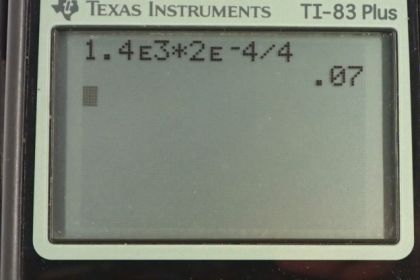
Calculator Screenshots

  • OpenStax College Physics, Chapter 11, Problem 55 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We have this formula for the pressure inside a spherical object and it's four times the surface tension divided by the radius of the object. We can solve this for gamma by multiplying both sides by r over four. Then we'll switch the sides around and we get gamma is pressure times radius over four. So that's 1.4 times ten to the three Pascals, times two times ten to the minus four meters radius of the alveolus, and divide by four and you get 0.07 newtons per meter is the surface tension. We're told that the surface tension of water at 20 degrees Celsius is 0.0728 and at 100 degrees Celsius it's 0.0589. This is pretty close to 20 degrees but slightly less. So it's tending towards this number here and so at some temperature probably between 20 and 100, well, we know that the temperature of the body is 37 degrees and so that's fluid. It's probably water at 37 degrees Celsius.