Question
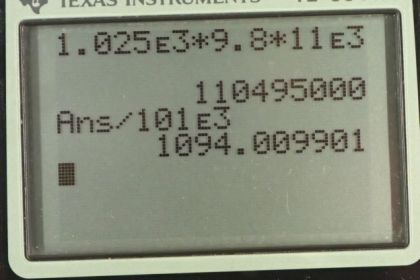
The greatest ocean depths on the Earth are found in the Marianas Trench near the Philippines. Calculate the pressure due to the ocean at the bottom of this trench, given its depth is 11.0 km and assuming the density of seawater is constant all the way down.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us to find the pressure at the bottom of the deepest part of the ocean, which is the Marian Trench in the Pacific near the Philippines. So it’s going to be the gauge pressure anyway which you know is all that really matters here because the pressure due to the atmosphere will be negligible in comparison to the enormous pressure of the high column of water. Now the pressure will be density of the sea water times g times the height. So density of sea water is 1.025 times ten to the three kilograms per cubic meter, and we make the assumption here that this density is constant over this great height, which is probably not exactly true, it’s likely that density gets a bit bigger at the bottom but never mind it’s close enough, times 9.8 newtons per kilogram, times 11 kilometers which is 11 times ten to the three meters, and this gives 1.10 times ten to the eight Pascals. Now that number is hard for us to understand because it’s just some big number, but we can turn it into something, a unit that we can relate to a bit better by multiplying by one atmosphere for every 101 times ten to the three Pascals, this works out to 1090 atmosphere so that’s really high pressure.