Question
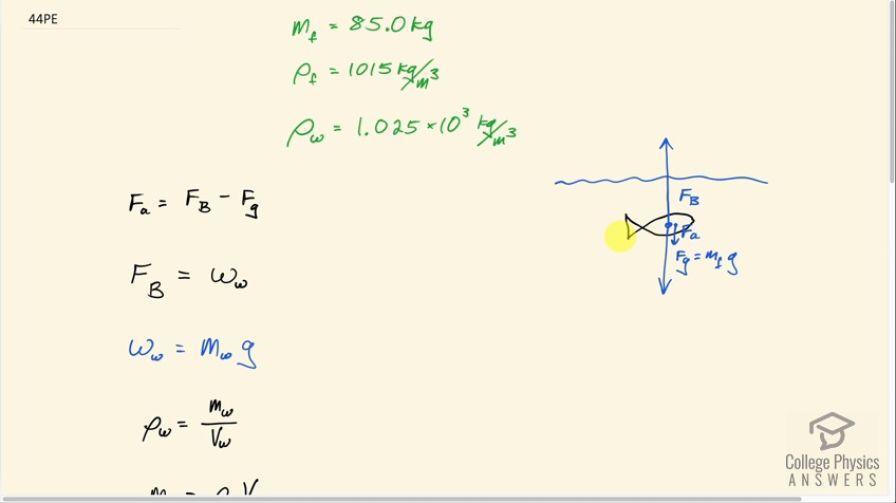
Some fish have a density slightly less than that of water and must exert a force (swim) to stay submerged. What force must an 85.0-kg grouper exert to stay submerged in salt water if its body density is ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
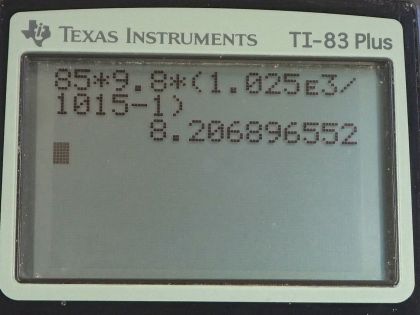
Video Transcript
This is College Physics Answers with Shaun Dychko. An 85.0 kilogram grouper fish is under seawater and it wants to stay submerged but it has a bit of a problem in that the buoyant force upwards is slightly bigger than gravity down and so this fish needs to apply some additional force to compensate for that difference. So this additional force down that the fish applies plus gravity has to equal the buoyant force upwards or, in other words, the applied force down is the difference between the buoyant force up and the gravity force down. We are given the density of the fish and we know the density of seawater —we can look up in table [11.1] and that's here, 1.025 times 10 to the 3 kilograms per cubic meter. So we need to figure out the buoyant force; the weight of the fish is straightforward because we are given the mass so we multiply that by g to find the weight and this buoyant force will take a bit of work and we have to use Archimedes principle. So this is Archimedes' principle here to say that the buoyant force is the weight of the water displaced by the fish and the weight of the water displaced is the mass of water displaced multiplied by g and we can figure out what volume of water is displaced because the volume of the fish since it's completely submerged is going to displace that volume of water so that's what I say down here... the volume of water displaced is the volume of the fish. But we can use volume to figure out the mass of water by knowing that the density of water is the mass of water displaced divided by the volume of water displaced and then we rearrange this for m by multiplying both sides by V and we have the mass is density of water times volume of water which we then substitute in to replace m w and we do that here. And since the fish is submerged, it's going to displace a volume of water equal to the fish's volume and that's going to be the mass of the fish divided by the density of fish. Rearranging this type of formula... I mean, you know, we have density of fish is mass of the fish divided by volume of fish and we can solve for V by multiplying both sides by V over ρ. Okay and that's where this comes from. So this is substituted in place of V w and so we have the buoyant force then weight of the water which is density of water times the mass of the fish divided by density of fish since that's the volume of water displaced times g and then we plug that in to here. So now the applied force then is this buoyant force minus gravity and we can factor out the mg from both terms. So we have mass of the fish times g times the ratio of densities minus 1 and that's 85.0 kilograms times 9.80 newtons per kilogram times 1.025 times 10 to the 3 kilograms per cubic meter— density of seawater— divided by 1015 kilograms per cubic meter— density of the fish—minus 1 which is 8.21 newtons. So the fish has to apply 8.21 N downwards in order to stay submerged.