Question
A certain man has a mass of 80 kg and a density of (excluding the air in his lungs). (a) Calculate his volume. (b) Find the buoyant force air exerts on him. (c) What is the ratio of the buoyant force to his weight?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 47 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
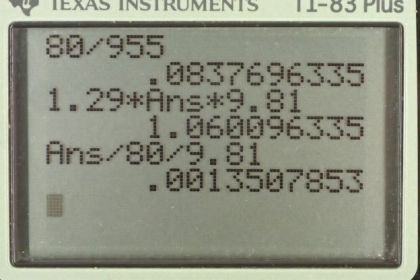
This is College Physics Answers with Shaun Dychko. We're going to rearrange the density formula to solve for volume. So density is mass divided by volume and we can multiply both sides by V over rho to solve for V. So V is mass over density so that's 80 kilograms divided by 955 kilograms per cubic meter which is the volume of 8.4 times ten to the minus two cubic meters. Part B asks us to find the buoyant force of air on the man. So the buoyant force will be the weight of air displaced by the man, that's Archimedes principle, and the weight of the air displaced will be the mass of air displaced times g. The mass of the air is going to be density times the volume of air displaced and the volume of air displaced will be the volume of the man which we calculated in part A already. So we substitute in density of air times the volume of the man in place of mass of the air times it by g. So that is 1.29 kilograms per cubic meter density of air, times 8.37696 times ten to the minus two cubic meters that's with lots of extra digits to avoid intermediate rounding error because we don't want to use 8.4. Multiply that by 9.81 newtons per kilogram and we get 1.06 newtons is the buoyant force. That's very small which is why you never really notice it. That as a fraction of the man's weight is going to be 1.06 newtons divided by 80 kilograms times 9.81 and that gives 0.0014 is the ratio between the buoyant force and the weight.