Question
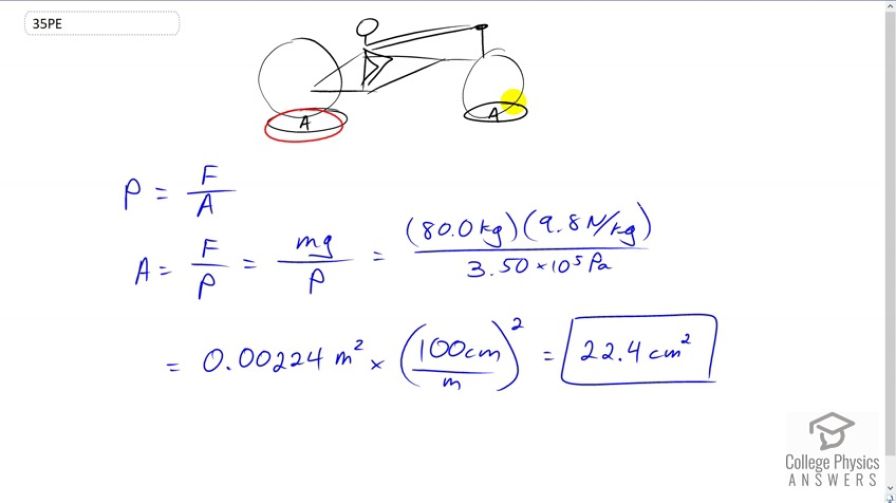
Assuming bicycle tires are perfectly flexible and support the weight of bicycle and rider by pressure alone, calculate the total area of the tires in contact with the ground. The bicycle plus rider has a mass of 80.0 kg, and the gauge
pressure in the tires is .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 35 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two bicycle tires and they have some area of rubber that’s in contact with the ground such that the pressure in the tire multiplied by that area provides the force needed to support this bicycle and rider. And the question is what is that area? And so we’ll multiply both sides of this pressure formula, which is force divided by area, by A over P and we’ll solve for A equals force divided by pressure. So the force needed is the total weight of the bicycle and rider, which we’re told is 80 kilograms mass and then multiply that by 9.8 newtons per kilogram, and then divide that by the gauge pressure in the tires which is 3.5 times ten to the five Pascals, that gives 0.00224 squared meters. And we’ll turn that into squared centimeters because that’s the unit that we can relate to a bit better. So we’ll multiply by 100 centimeters for every meter, and we’ll do that multiplication twice in order to convert meters squared into centimeters squared, and that is 22.4 squared centimeters in total area among the two tires needed to support the weight of the bicycle and rider given this particular pressure. And now if the pressure is higher by the way, you would require less area because area is inversely proportional to pressure, pressure in the denominator, this is why competitive road cyclists will have very high pressure tires in their bicycles in order to minimize the amount of area contact with the ground because that also reduces a little bit of the rolling friction.
