Question
A crass host pours the remnants of several bottles of wine into a jug after a party. He then inserts a cork with a 2.00-cm diameter into the bottle, placing it in direct contact with the wine. He is amazed when he pounds the cork into place and the bottom of the jug (with a 14.0-cm diameter) breaks away. Calculate the extra force exerted against the bottom if he pounded the cork with a 120-N force.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 26 (Problems & Exercises)
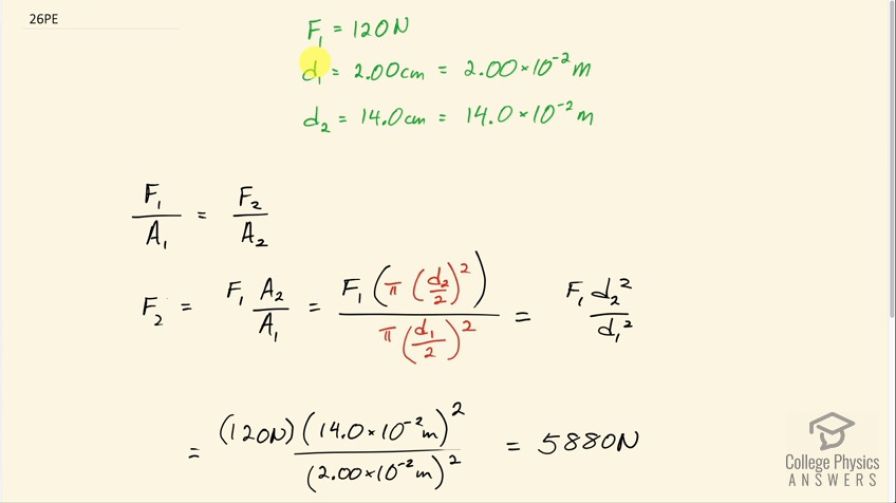
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A cork is pounded into the top of a jug of wine with a force of 120 newtons and the diameter of the cork is 2.00 centimeters and the diameter of the bottom of the jug is 14.0 centimeters and this bottom pops off and we are meant to calculate how much force beyond the 120 newtons applied is on the bottom of the jug? So we convert these centimeters into meters although it turns out that's not really necessary since we are just dividing the squares of these numbers and so it just matters that the units are the same but I did it out of a matter of habit. So we know that the pressure where the cork is will be same as the pressure at the bottom of the jug and I have written pressure as force divided by area here. So this is the F 1, which is the force applied to the cork divided by the area of the cork and that's going to equal the force applied to the bottom of the jug, F 2, divided by the area of the bottom of the jug, A 2. So we want to know what F 2 is and so we'll multiply both sides by A 2 to solve for it then switch the sides around. So F 2 is F 1 times A 2 over A 1; the area of the bottom of the jug will be π times the radius of the circular bottom squared and the radius is half the diameter and then same for the A 1—same formula— but d 1 instead of d 2. The π's cancel and so do these denominators which will end up being 4 after you square the denominators; they cancel and we are left with F 1d 2 squared over d 1 squared. So that's 120 newtons applied times 14.0 times 10 to the minus 2 meters— diameter of the bottom of the jug—squared divided by 2.00 times 10 to the minus 2 meters—for the cork—squared and that's 5880 newtons. And to find the extra force, we take 120 newtons away from that and this is the amount by which the force on the bottom of the jug exceeds the force applied and that's 5760 newtons.
