Question
(a) Calculate the buoyant force on a 2.00-L helium balloon. (b) Given the mass of the rubber in the balloon is 1.50 g, what is the net vertical force on the balloon if it is let go? You can neglect the volume of the rubber.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 45 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
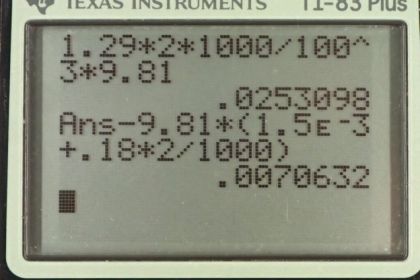
This is College Physics Answers with Shaun Dychko. We're going to calculate the buoyant force on this two liter helium balloon. The buoyant force will be the weight of air that it displaces because that's Archimedes principle, and the weight of the air displaced will be the mass of the air times g. So let's create an expression for the mass of the air in terms of volume because we know the helium balloon is a two liter volume and so we know the volume of air displaced, convert that into a mass. So the density of air is the air's mass divided by the air's volume. We can solve this for mass of the air by multiplying both sides by the volume of the air displaced. So mass air is air density times volume, and the air volume is the balloon's volume, that's how much air is displaced because the balloon's totally submerged in the air you could say. Nobody ever says that but that's -- what's happened here is the balloon is in the air. All right. So we'll substitute V balloon for volume and we have the density of air and all this is replacing mass of the air in our buoyant force formula. So that is 1.29 kilograms per cubic meter density of air, times two liters converted into cubic meters and multiply by 1000 cubic centimeters per liter and then by one meter for every 100 centimeters cubed, and multiply by g and we get 2.53 times ten to the minus two newtons is the buoyant force. Now the net force on the balloon will be this buoyant force minus the force of gravity on the rubber and then also minus the force of gravity on the helium contained inside the balloon. So we have buoyant force minus mass of the rubber times g, minus mass of the helium times g, and you can factor out the g here. So we have g times the sum of the rubber and helium masses. Now the mass of the rubber we're given so that part's easy, but the mass of the helium we'll have to figure out in terms of the helium's density and its volume. So the density of helium is the helium mass divided by helium volume. We'll solve this for the mass by multiplying both sides by the volume of the helium. So the mass of the helium is density of the helium times the helium volume which we substitute in for mass he here. Then we plug in numbers. So 0.0253098 newtons which we calculated in part A, the buoyant force, minus 9.81 newtons per kilogram, g, times 1.5 grams which gets converted into kilograms by multiplying by ten to the minus three, then plus the density of helium of 0.18 kilograms per cubic meter, times two liters converted into cubic meters by multiplying by one cubic meter for every 1000 liters. It's a bit of a faster way of converting compared to what is up here but it's equivalent. This works out to 7.07 times ten to the minus three newtons is the net force on the balloon. So it's a net force upwards so the balloon will rise but it won't rise very quickly because this is a very small force.