Question
(a) Verify that work input equals work output for a hydraulic system assuming no losses to friction. Do this by showing that the distance the output force moves is reduced by the same factor that the output force is increased. Assume the volume of the fluid is constant. (b) What effect would friction within the fluid and between components in the system have on the output force? How would this depend on whether or not the fluid is moving?
Final Answer
- Please see the solution video.
- Friction would make the work done in the slave cylinder () less than the work done on the master cylinder () since energy would be lost to friction. This is true only when the fluid is moving. Since , is reduced since . must stay the same, with or without friction, since the same volume of fluid would be displaced from one cylinder to the other, which means must reduce in order to make .
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
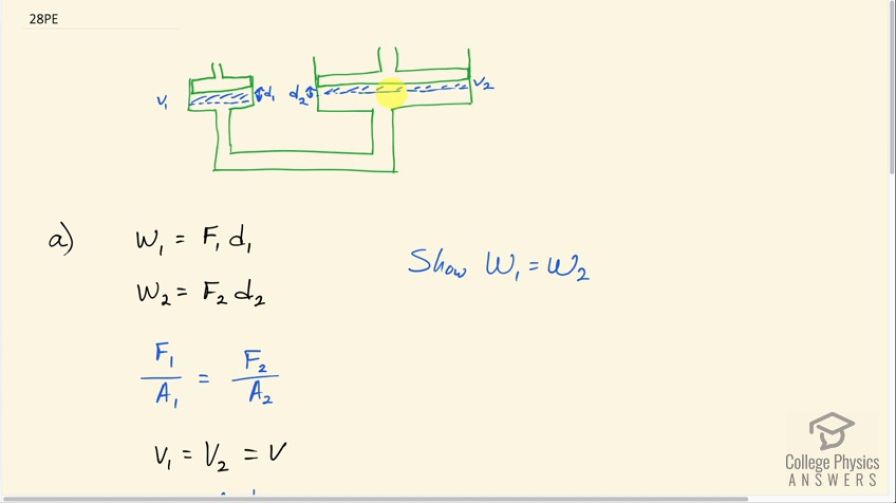
This is College Physics Answers with Shaun Dychko. We are going to show how the work done in a hydraulic system by the first piston is the same as the work done on the second piston. So the work done will be the force, F 1, applied down on this first piston multiplied by the distance traveled, d 1 and the work done on the second piston will be the force applied on it, F 2, which is going up like this times its distance traveled, d 2... we have F 1 down here and F 2 up here... and this volume of fluid displaced on the left side will equal the volume of fluid that appears on the right hand side because the fluid can't just disappear; whatever is reduced from here, increases here. So that means this V 1 equals V 2; these two volume's are the same. So work done on piston 1 is F 1 times d 1 and work done on piston 2 is F 2 times d 2 and we are gonna show that these two amounts of work are the same and we need to relate these distances traveled by the piston's using Pascal's principle which is to say that the pressure in one part of the fluid is the same as the pressure in the other part of the fluid. So F 1 divided by A 1 equals F 2 divided by A 2— area of this piston. So the volume's are the same and the volume in the first case is area 1 times the displacement 1 and volume in the second case is area 2 times displacement 2 and area 1 is then V divided by d 1 or I divided this by d 1 and this side by d 1 and I didn't bother writing a subscript 1 for this volume because the volume's are the same; there's no need to distinguish 1 versus 2 since they are equal. So A 1 is V over d 1 and A 2 is V over d 2 and these can be substituted in for the area's in this Pascal's principle. So when dividing by A 1, I am going to instead multiply by the reciprocal of A 1 since I don't like to divide a fraction by a fraction so I'm going to multiply by the reciprocal of A 1 which is d 1 over V. And likewise for the right hand side, replacing A 2 with d 2 over V after taking its reciprocal since we are multiplying and the V's cancel and this is to say that F 1d 1 equals F 2d 2 but F 1d 1 is the work done by the first piston and F 2d 2 is the work on the second piston and they are the same so w 1 equals w 2. Now if there is friction, this w 2 would be less than w 1 since some energy would be lost to friction and this is true only when the fluid is moving because there's no static friction with the fluid; it's kinetic friction that would be an issue here. So because this w 2 is less than w 1, F 2 has to be reduced because w 2 is F 2 multiplied by d 2 but d 2 will stay the same since the same volume of fluid will be displaced from one cylinder to the other so so it's F 2 that has to vary here in order to reduce w 2 and so it will vary by being reduced in order to make w 2 less.