Question
Gauge pressure in the fluid surrounding an infant’s brain may rise as high as 85.0 mm Hg (5 to 12 mm Hg is normal), creating an outward force large enough to make the skull grow abnormally large. (a) Calculate this outward force in newtons on each side of an infant’s skull if the effective area
of each side is . (b) What is the net force acting on the skull?
Final Answer
- The net force is zero since the skull is stationary. The cohesion of the skull balances the force due to the outward gauge pressure.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 72 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
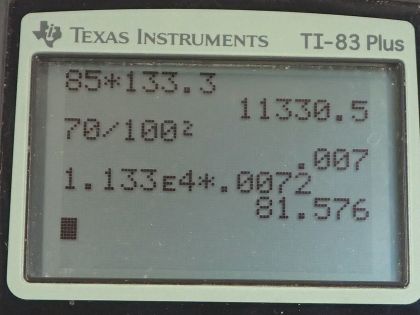
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The infants skull might have a gauge pressure of 85.0 millimeters of mercury due to the fluid surrounding the infants brain and we are gonna convert that into pascals by multiplying by 133.3 pascals per mm Hg and we have 1.133 times 10 to the 4 pascals. And the area of each side of the infants skull is 70.0 square centimeters and we convert that into meter squared by multiplying by 1 meter for every 100 centimeters and we do that multiplication twice and that works out to 0.0072 square meters. So notice that I have converted units at this stage of writing down the information that we know; it's nice to get it out of the way here so we don't have to worry about unit conversions when we are thinking about how to do the work. So in part (a), we are gonna figure out what force is applied on one side of the skull and pressure is force divided by area so we can solve this for force by multiplying both sides by area and we end up with force is pressure times area. So that's this pressure that we found, after converting to pascals, multiplied by this area is 81.6 newtons. Now this is the gauge pressure in the infants brain which is to say it's the amount by which the pressure already exceeds atmospheric pressure. So that means you can't say that the net force is zero because the atmosphere balances this pressure because the atmosphere already balances a portion of the absolute pressure inside the brain and this pressure is the amount that the pressure in the brain exceeds the atmospheric pressure. So atmospheric pressure is already taken into account and this is the amount that the pressure inside exceeds that atmospheric pressure. So this has to be balanced by something else and it has to be balanced because the skull is stationary so that means there's no acceleration and no net force and it's being balanced by the cohesion of the skull material; the integrity of the bone balances the force due to this gauge pressure.