Question
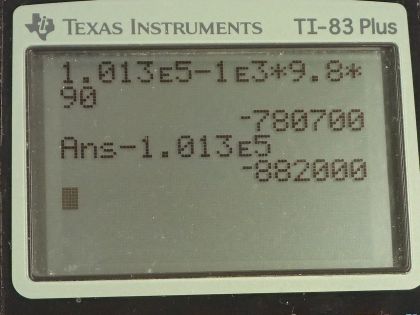
Some miners wish to remove water from a mine shaft. A pipe is lowered to the water 90 m below, and a negative pressure is applied to raise the water. (a) Calculate the pressure needed to raise the water. (b) What is unreasonable about this pressure? (c) What is unreasonable about the premise?
Final Answer
- It is normally not possible to create a negative gauge pressure below -1 atm (-1.013 \times 10^{5}\textrm{ Pa})
- Water cannot be removed this way. Either it can be done in many smaller stages, or a large positive pressure can be applied from below.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 84 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Some miners want to remove some water from 90 meters below the ground and they have some machine here which is exerting some sort of negative pressure to suck the water up this column, up this pipe, and it has subscript m for 'machine' and there is a pressure due to this water and due to the weight of the water and that has an amount density of water times g times the height of the column and then there's this atmospheric pressure that's pushing all the water down and the total of the machine's pressure and the pressure of the water column has to equal the pressure of the atmosphere when this column is just stationary in there. And so that means the machine pressure is gonna be pressure of the atmosphere minus pressure of the water column. So we substitute in ρgh in place of the pressure of the water column and then we get that the pressure the machine has to have here in this space is the atmospheric pressure—1.013 times 10 to the 5 pascals— minus the density of water times 9.80 newtons per kilogram times 90 meters—height of the water column— and that is negative 7.807 times 10 to the 5 pascals. And this is the absolute pressure and it's possible that the question is asking for gauge pressure and in which case, let's write our answer in terms of gauge pressure. So we have absolute pressure is gauge pressure plus atmospheric pressure and we solve for gauge pressure by subtracting atmospheric pressure from both sides. And so we have the absolute pressure that we found here minus the atmospheric pressure, which is negative 8.8 times 10 to the 5 pascals— this is the gauge pressure. So it's normally not possible to create such a large magnitude negative pressure; if you evacuate this space completely of all air then your gauge pressure will be negative 1 atmosphere. So this is, you know, almost negative 8 atmospheres which is just not really possible unless you have a very special thing like we saw in question 80 or so? Yeah this thing... we have special substance that the water tends to bond to and you yank up this plunger and it will create a negative pressure in here in this fluid but only because of these special circumstances where the water is bonding to this plunger material. Okay! So normally not possible to go below negative 1 atmosphere gauge pressure. So that means water cannot be removed this way, it has to be done in many smaller stages. The pressure head of water is about 10 meters which is to say that you know using suction, the maximum height you can bring a water column is 10.0 meters up. So you would have to bring it 10.0 meters up and then dump it into a little pool and then have a second pipe taking it another 10.0 meters, dump it into a pool and have a third pipe another 10.0 meters and so on. Or you can create a large positive pressure from below and push the water column up; there's no limit to, I mean... it's possible to make very high positive pressures so this is possible.