Question
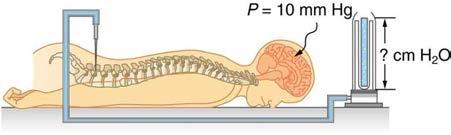
Pressure in the spinal fluid is measured as shown in Figure 11.46. If the pressure in the spinal fluid is 10.0 mm Hg: (a) What is the reading of the water manometer in cm water? (b) What is the reading if the person sits up, placing the top of the fluid 60 cm above the tap? The fluid density is 1.05 g/mL.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 75 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The pressure reading in the water manometer is going to be 10 millimeters of mercury converted into centimeters of water. So we have a conversion factor that's given to us in the textbook between millimeters of mercury and Pascals, and then again from Pascals to centimeters of water. So we have 133 Pascals for every one millimeter of mercury and then we multiply that by one centimeter of water for every 98.1 Pascals. We end up with 13.6 centimeters of water. Now if the person sits up then they will be adding an additional pressure due to the height of the column of spinal fluid. So we have to figure out what this term is and then add that to P naught which is this pressure when lying down. So this is P naught here. So rho g h, well, we need to change this density into kilograms per cubic meter. So we have 1.05 grams per milliliter and then we convert that into centimeters cubed, then turn that into meters cubed on the bottom by multiplying by 100 centimeters for every meter three times, and then we multiply by one kilogram for every 1000 grams. We're left with kilograms per cubic meter. Then multiply by g which is 9.81, then times the height in meters, so 60 centimeters times one meter for every 100 centimeters. Then we want to convert this into centimeters of water. So there's one centimeter of water for every 98.1 Pascals. This makes 63 centimeters of water. So we add that to 13.6 centimeters when lying down. This works out to 76.6 centimeters of water.
