Question
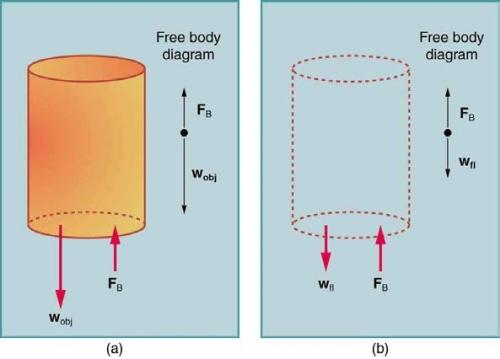
Referring to Figure 11.20, prove that the buoyant force on the cylinder is equal to the weight of the fluid displaced (Archimedes’ principle). You may assume that the buoyant force is and that the ends of the cylinder have
equal areas . Note that the volume of the cylinder (and that of the fluid it displaces) equals .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 52 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to prove that the buoyant force is the weight of fluid displaced by the object and this is Archimedes principle. So we are told to assume that the top and bottom face of the cylinder are of equal areas A and there is force F 2 upwards here and then force F 1 downwards at the top surface and this difference between these two forces is the buoyant force. So this F 2 is greater since the pressure deeper is higher and whereas here, this surface is at a shallower depth and so its pressure is less there and so there's less force. So the buoyant force is that difference and F 2 is gonna be the pressure at this bottom depth multiplied by the area and then the force on the top face will be the pressure at that depth, P 1, times that same area A and we can factor out the area and the pressure is the density of the fluid times gravitational field strength times the height so P 2 is ρgh 2 and P 1 is ρgh 1 and we can substitute for each of those now on this line here and this ρ and the g can be factored out. So we have area times density of the fluid times g times the difference in heights. Now the volume of the object is equal to the volume of the fluid displaced because this object is in the water now completely, or whatever fluid it is, it's completely in the fluid and it's going to displace volume of fluid equal to the volume of the object. And the volume of this object is its area multiplied by its height— that's the volume of a cylinder; it's the area of the circular face multiplied by the height of the cylinder. So we can substitute that in place of A times h 2 minus h 1 and so the buoyant force then is the volume of the fluid times the density times g and the volume times the density is the mass and it's being multiplied by g here and so that is the weight of the fluid displaced and therefore, we have shown that the buoyant force is the weight of the fluid displaced and that is Archimedes principle.