Question
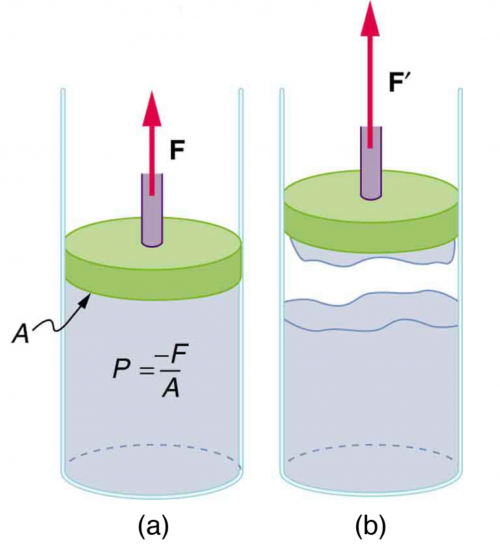
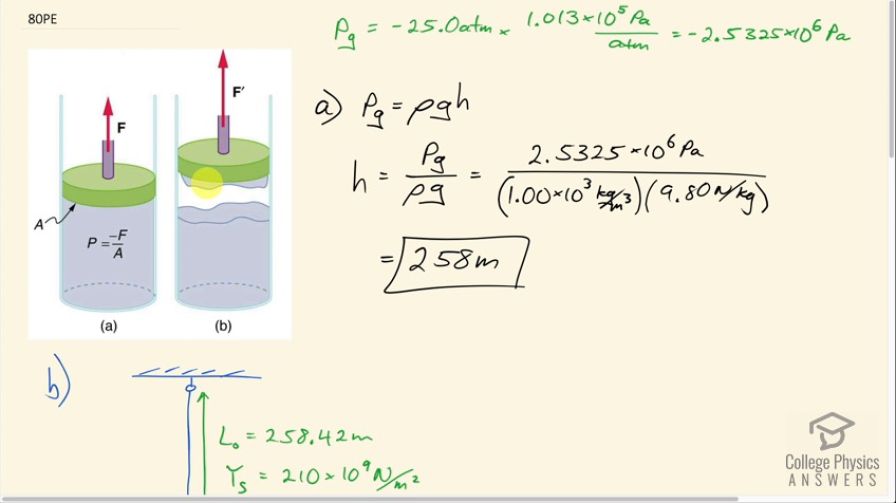
A negative pressure of 25.0 atm can sometimes be achieved with the device in Figure 11.43 before the water separates. (a) To what height could such a negative gauge pressure raise water? (b) How much would a steel wire of the same diameter and length as this capillary stretch if suspended from above?
Final Answer
Note: at 0:14 Shaun misspoke in saying the gauge pressure was -27 atmospheres. In fact, it is -25 atmospheres as written.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 80 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This here's a strange device that must have some special materials chosen such that the water sticks to this surface and it's pulled upwards and creates a very large negative gauge pressure of negative 25.0 atmospheres. We convert that into pascals and then question (a) asks us to what height would a column of water be raised with this hypothetical negative 25.0 atm gauge pressure? So we can divide both sides of this by density of water times g and the height then is this pressure divided by density times g. So we have 2.5325 times 10 to the 6 pascals divided by density of water multiplied by g and that is 258 meters. In part (b) we are asked suppose you have a steel wire that is the same length as this column of water from part (a), 258.42 meters, how much would this wire stretch just due to gravity by hanging there? So we need to look up the Young's modulus for steel and that's something we find in table [5.3]—this is from chapter 5— and the Young's modulus for steel is 210 times 10 to the 9 newtons per square meter and then we have this formula to say that the force per cross-sectional area of the wire equals the Young's modulus times its stretching amount divided by its original length, L naught. So we are gonna solve for ΔL here by multiplying both sides by L naught over Young's modulus. And we get the ΔL is L naught F over Y—Young's modulus—times A. So we need to know what this force then is; this force is the way to the wire and so that's mg but we don't know what the mass is, all we know is its length, and so we replace mass with by rearranging this density formula and density is mass per volume and we multiply both sides by V and we get the mass is density times volume. So then our force becomes ρVg but we also don't know what the volume is but we can replace it with L naught times A— L naught being the length and A being the cross-sectional area and so this is like a cylinder so we have the area of the base times its length is the volume— so we replace V with that, L naught A here, so all of this can be written in place of F in this formula for ΔL. So I am rewriting ΔL is L naught times ρL naught A times g substituting for F here all divided by Young's modulus times A and what's nice is that this cross-sectional area, which we also don't know, cancels and we are left with ρ times L naught squared times g over Y all of which we know. So we have 7.8 times 10 to the 3 kilograms per cubic meter is the density of steel— that's what we found in table [11.1]— (where is that... right here) and then we have times the length— 258.42 meters—squared times 9.80 newtons per kilogram divided by Young's modulus and this makes a stretch of 2.4 centimeters.
