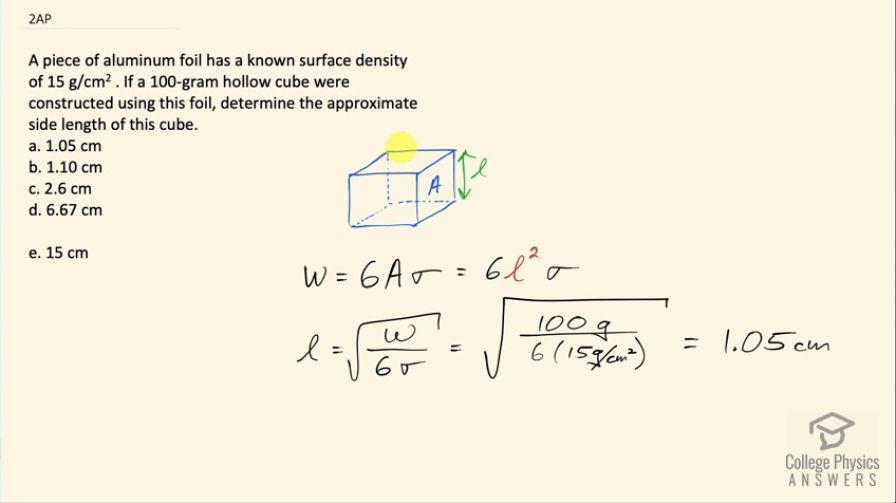
A piece of aluminum foil has a known surface density of $15{\text{ g/cm}}^2$. If a 100-gram hollow cube were constructed using this foil, determine the approximate side length of this cube. (a) 1.05 cm
(b) 1.10 cm
(c) 2.6 cm
(d) 6.67 cm
(e) 15 cm

Video Transcript

This is College Physics Answers with Shaun Dychko. A piece of aluminum foil has a known surface density of 15 grams per square centimeter, we want to have a 100-gram hollow cube constructed from this foil and what should the side length of the cube be such that we are using a foil with this surface density and achieving a hollow cube with this weight? So a cube has six sides, each side will have an area A and so the total weight of the cube will be 6 times the area of a single side multiplied by the surface density, which I will call σ and the area per side is l squared so we have 6l squared times σ— l being the side length— and then we can solve for l by dividing both sides by 6σ and then take the square root of both sides and that is then the side length is the square root of the weight divided by 6 times the surface density. So square root of 100 grams divided by 6 times 15 grams per square centimeter that works out to 1.05 centimeters and we know that our final unit will be in centimeters since we used centimeters squared here in our work and so the answer is (a) 1.05 centimeters.