Question
Calculate the pressure due to the ocean at the bottom of the Marianas Trench near the Philippines, given its depth is 11.0 km and assuming the density of sea water is constant all the way down. (b) Calculate the percent decrease in volume of sea water due to such a pressure, assuming its bulk modulus is the same as water and is constant. (c) What would be the percent increase in its density? Is the assumption of constant density valid? Will the actual pressure be greater or smaller than that calculated under this assumption?
Final Answer
- decrease in volume
- increase in density. The actual pressure will be greater than calculated in part (a) since, with greater density, there will be greater mass, and thus weight, in the vertical column of water. This greater weight will cause greater pressure.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 82 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
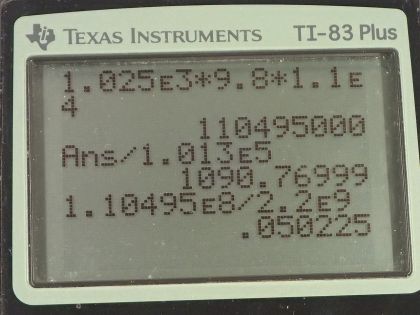
This is College Physics Answers with Shaun Dychko. We are going to calculate the pressure at the bottom of the Mariana trench which is 11.0 kilometers below sea level and we convert that into meters. The density of seawater we look up in our table [11.2] and it is 1.025 times 10 to the 3 kilograms per cubic meter and the pressure or the gauge pressure and that is to say the amount of pressure in excess of the atmospheric pressure is the density of the fluid times acceleration due to gravity times the height of the fluid column and so that's 1.025 times 10 to the 3 kilograms per cubic meter times 9.80 newtons per kilogram times 1.10 times 10 to the 4 meters—height— and that is this many pascals which we convert into atmospheres by multiplying by 1 atm for every 1.013 times 10 to the 5 pascals and that is 1.09 times 10 to the 3 atmospheres. So that's a 1090 atm of pressure at the bottom of the Mariana trench—that's huge! And it was okay to just ignore atmospheric pressure and just talk about the gauge pressure and I guess the question is sort of asking just for the gauge pressure because it says "what's the pressure due to the seawater?" and so suggesting that just the gauge pressure is enough. We could add 1 atmosphere to that but you wouldn't even see it because it's not one of the significant digits in the ones place here. Okay! Part (b) says calculate the percent decrease in volume of the seawater due to this pressure. So we have to look back to chapter 5 and we say that the change in volume divided by the original volume in other words, the fractional change in volume is 1 over the Bulk modulus of the material multiplied by the force per area applied on the material but force per area is pressure so we are gonna write P in place of F over A and so we look up the Bulk modulus for seawater and it is 2.2 times 10 to the 9 newtons per square meter and so we have 1.10495 times 10 to the 8 pascals which we reuse in this figure here because we want mks units—meters, kilograms and seconds type units here— and divide it by the Bulk modulus and that is 0.05023 which is 5.0 percent and that's a decrease in volume. There's no negative sign in this formula but it's just understood that this is a decrease in volume. And so the next question in part (c) is what is the percent change in the density because since the volume is changing and the masses can stay the same... the masses being squished into a smaller volume now so its density is going to increase and so by how much is the question? So we have this final density which will be some mass divided by the original volume plus this change minus the original density which is mass divided by original volume all divided by the original density and then we can divide this term by this term to make 1 and this term divided by this is the same as this multiplied by its reciprocal so times by V naught over m and the m's cancel and we are left with V naught over V naught plus ΔV. Okay... and all this is minus 1. And then divide top and bottom by 1 over V naught and that's convenient because we end up with this expression where we have this term which we have already calculated. So we have 1 over 1 plus the fractional change in volume and I have introduced the negative sign there because our understanding is that this is a decrease so we can just put it there and this all works out to 0.05289. So this is an increase in density, 5.3 percent. And now because we have noticed that the density is going to increase by a significant amount— 5.3 percent is significant— the actual pressure for part (a) is going to be greater than what we have calculated because our calculation makes the assumption that the density is constant over this entire vertical column of seawater— this 11.0 kilometer high column of seawater— but in our work here in parts (b) and (c), we can see that the density is not constant and so the actual pressure will be greater because with greater density, there's gonna be greater mass stuffed into the given volume and therefore the weight of this vertical column will be greater and therefore its pressure will be greater.