Question
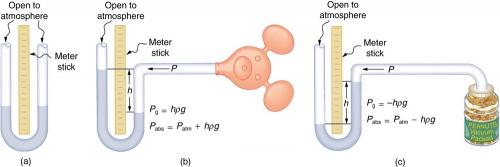
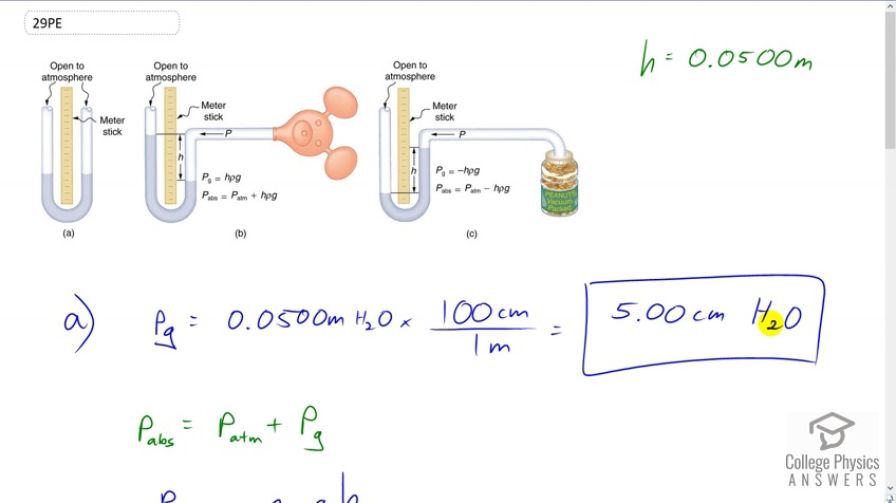
Find the gauge and absolute pressures in the balloon and peanut jar shown in Figure 11.19, assuming the manometer connected to the balloon uses water whereas the manometer connected to the jar contains mercury. Express in units of centimeters of water for the balloon and millimeters of mercury for the jar, taking for each.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 29 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
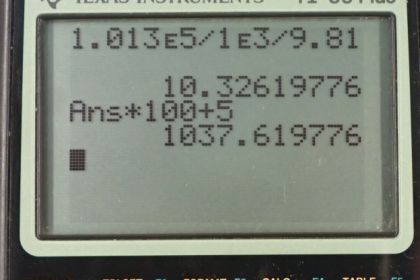
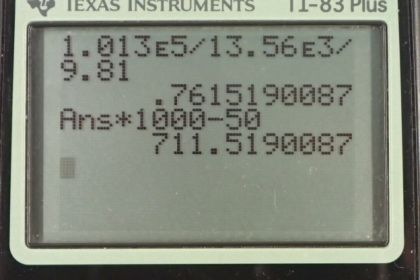
This is College Physics Answers with Shaun Dychko. In part A of this question, we're asked to find what is the gauge pressure in this balloon in centimeters of water, then find the absolute pressure in centimeters of water. Then in part B, we'll find the gauge pressure of the vacuum in this peanut jar in millimeters of mercury, then the absolute pressure in millimeters of mercury. So the height of this -- the height difference between the two levels of the fluid in this manometer is 0.05 meters we're told and so the gauge pressure in part A is going to be 0.05 meters of H2O times 100 centimeters per meterand the meters cancel. This gives us 5.00 centimeters of H2O because the manometer directly is measuring gauge pressure because it is open to the atmosphere. Now the absolute pressure is the atmospheric pressure plus this gauge pressure. So, we need to figure out what is atmospheric pressure in centimeters of water and then we'll add that to the answer to the gauge pressure that we already have in centimeters of water. So atmospheric pressure is density of water times g times the height of a column of water that you'd have if you're measuring atmospheric pressure. We'll solve for h atm by dividing both sides by rho w g. So that is atmospheric pressure which is 1.013 times ten to the five newtons per meter squared divided by the density of water which is one times ten to the three kilograms per cubic meter times 9.81 and we get 10.326 meters of water. Those meters have to be converted into centimeters by multiplying by 100 and we add that to five and then we have the absolute pressure which is 1.038 times ten to the three centimeters of water. Then the gauge pressure in the peanut jar in terms of millimeters of mercury is negative because it's a vacuum and its level open to the atmosphere is below the level over here. So that's negative 0.05 meters of mercury times 1000 millimeters per meter giving us negative 50.0 millimeters of mercury as the gauge pressure. The absolute pressure will be the atmospheric pressure plus the gauge pressure. Now you could look up atmospheric pressure in millimeters of mercury, it's 760, but I'm calculating it here anyway. So atmospheric pressure is the density of mercury times g times the height of the mercury column when measuring the atmospheric pressure. So we divide both sides by the density times g and we get 1.013 times ten to the five newtons per meter squared divided by 13.56 times ten to the three kilograms per cubic meter density of mercury, times 9.81 and gives 0.76152 meters of mercury. So multiply that by 1000 to convert into millimeters and subtract from the 50 and you get 712 millimeters of mercury is the absolute pressure.