Question
The pressure exerted by a phonograph needle on a record is surprisingly large. If the equivalent of 1.00 g is supported by a needle, the tip of which is a circle 0.200 mm in radius, what pressure is exerted on the record in ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 12 (Problems & Exercises)
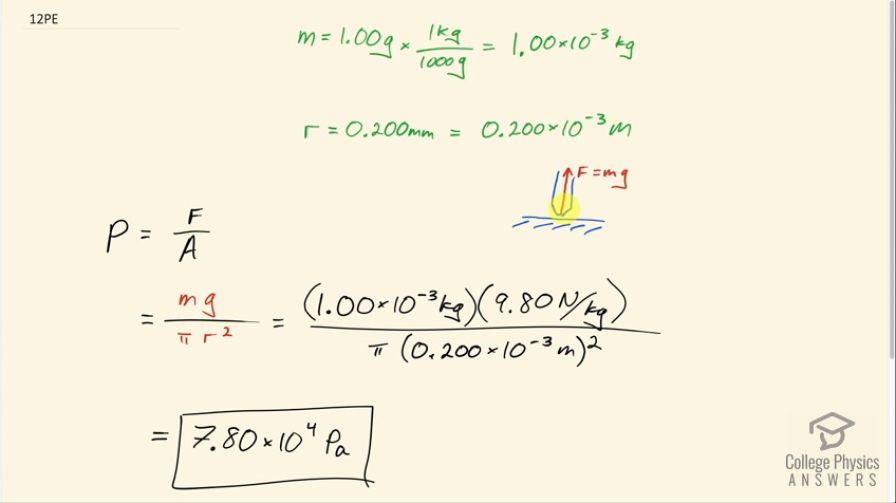
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The needle of a record player is being supported by the normal force due to the record and that normal force is going to equal the force of gravity pulling it down and the mass is 1.00 gram which we'll convert into kilograms by multiplying by 1 kilogram for every 1000 grams. The radius of the needle—if we were to look at the end of it—is a circle and it has this radius here of 0.200 millimeters and we'll convert that into 0.200 times 10 to the minus 3 meters because the prefix 'milli-' means times 10 to the minus 3. And this area of the circle is going to be πr squared and we can figure out the pressure then. So the pressure is the force per area so the force is mg and the area is πr squared so we have 1.00 times 10 to the minus 3 kilograms times 9.80 newtons per kilogram divided by π times its radius in meters squared and that is 7.80 times 10 to the 4 pascals.
