Question
One way to force air into an unconscious person’s lungs is to squeeze on a balloon appropriately connected to the subject. What force must you exert on the balloon with your hands to create a gauge pressure of 4.00 cm water, assuming you squeeze on an effective area of ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 70 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
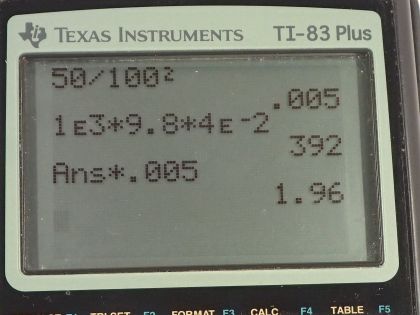
This is College Physics Answers with Shaun Dychko. When using a balloon to inflate a person's lungs, the pressure in the balloon is 4.00 centimeters of water— this is the gauge pressure, the pressure by which the pressure in the balloon exceeds atmospheric pressure— and the area over which a person's hand is touching the balloon is 50.0 square centimeters which we convert into meter squared by multiplying by 1 meter for every 100 centimeters twice that is 0.00500 square meters. So this pressure has a very unusual unit of cm H 2 O so we have to turn that into pascals and we'll do that by multiplying by the density of water times gravitational field strength times height because this is the gauge pressure of a column of fluid. And so we have the density of water is 1.000 times 10 to the 3 kilograms per cubic meter times 9.80 newtons per kilogram times the height converted into meters by multiplying by times 10 to the minus 2; this works out to 392 pascals. So then we return to this formula, pressure is force per area, and we solve for F by multiplying both sides by A. So F is P times A; 392 pascals times 0.00500 meter squared and that's 1.96 newtons has to be applied to the balloon.