Question
An under-inflated volleyball is pumped full of air so that its radius increases by 10%. Ignoring the mass of the air inserted into the ball, what will happen to the volleyball's density?
- The density of the volleyball will increase by approximately 25%.
- The density of the volleyball will increase by approximately 10%.
- The density of the volleyball will decrease by approximately 10%.
- The density of the volleyball will decrease by approximately 17%.
- The density of the volleyball will decrease by approximately 25%.
Final Answer
(e)
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 1 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
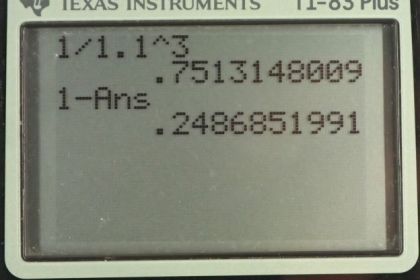
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. So a volleyball is going to be pumped full of air so that its radius increases by ten percent. We want to find out what is its new density, how does its new density compare to its old density? What is the percent change in density, in other words. Well, the answer is E as I've circled there but let me explain why. So density is mass divided by volume and that is mass divided by volume of a sphere which is four thirds pi r cubed, radius cubed. We'll multiply top and bottom by three and we get three m over four pi r cubed. So in the first case we have density one is three m over four pi r one cubed, and in the second case, we have the same mass because we're told to ignore the mass of the air that's inserted into the ball. So that's three m with no subscript needed, divided by four pi r two cubed. Now we're told that r two is ten percent more than r one, so that's going to be r one plus 0.1 times r one which is 1.1 r one. So we'll substitute that in for r two and we get density two is three m over four pi 1.1 r one, all cubed. So if we divide these two densities, that is three m over four pi 1.1 r one cubed, that's rho two. Then we're going to divide by density one, we're going to multiply by its reciprocal. So that's four pi r one cubed over three m. This works out to one over 1.1 cubed because so many other things cancel even the r one cubed cancel. This is 0.751. So the new density will be 0.75 times the old density. Now to find the percent change, we take the change in density divided by the original density. So that's rho two minus rho one, all over rho one which is rho two over rho one minus one when you divide this into both terms in the numerator. This is what we just calculated here. Minus one gives us a negative 0.25. So this is a decrease in density of 25 percent and that's answer E.