Question
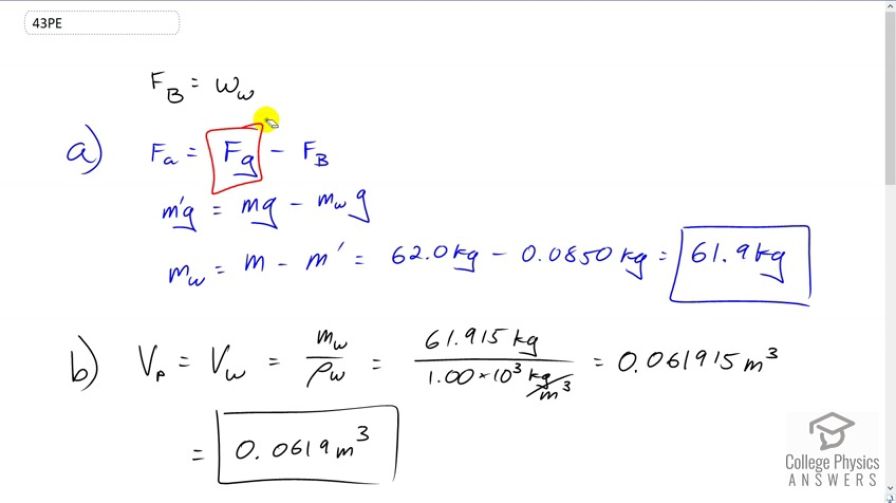
In an immersion measurement of a woman's density, she is found to have a mass of 62.0 kg in air and an apparent mass of 0.0850 kg when completely submerged with lungs empty. (a) What mass of water does she displace? (b) What is her volume? (c) Calculate her density. (d) If her lung capacity is 1.75 L, is she able to float without treading water with her lungs filled with air?
Final Answer
- Yes, they will float without treading water.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
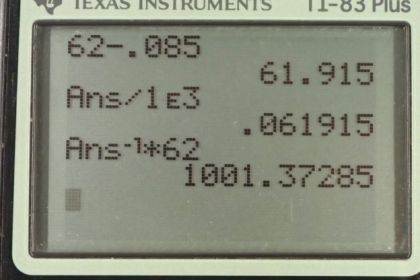
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The apparent weight of this woman is her true weight when she's not in the water, and you know, we can neglect the fact that there is a buoyant force applied by air that's pretty negligible, so we call that true weight then, minus the buoyant force provided by the water. This buoyant force is the weight of the water displaced by the woman, that is Archimedes principle. We're going to figure out the mass of water displaced by substituting for each of these forces. So the apparent weight will be the apparent mass m prime times g. That equals the real mass times g, minus the buoyant force which is the weight of the water displaced which is the mass of the water displaced times g. We'll solve for m w by dividing everything by g and then add the resulting m w to both sides and subtract m prime from both sides. We have m w is her true weight minus her apparent weight, or her true mass minus apparent mass. So 62 kilograms minus 0.085 kilograms which is 61.9 kilograms is the mass of water displaced. Now the volume of the person will be the volume of water displaced more or less because she's pretty much all submerged and so that's 61.915 kilograms divided by this density of water, one times ten to the three kilograms per cubic meter which is 0.061915 meters cubed. We'll round that to 0.619 cubic meters. Now this doesn't require -- well, never mind. I was going to say it doesn't require that she's all submerged but it does actually require that she's submerged because in order for her volume to be the same as the volume of the water displaced, she has to be all submerged which she nearly is which is -- maybe we should write that approximately equals there, something like this. There. Then her density is her mass divided by her volume so that's 62 kilograms over 0.061915. That gives one times ten to the three kilograms per cubic meter which is no surprise because she's nearly all submerged so she's not really floating, so her density should be close to that of water. If she fills up her lungs with one and three quarter liters of air, will she be able to float without treading water is the question now. So we're going to find her density. So her total mass will be the mass that she had before plus the mass of air in her lungs which is probably negligible but we'll put it in there anyway, divided by her original mass plus her volume plus the volume of air that she puts into her lungs. So the volume of air is one and three quarter liters times 1000 cubic centimeters for every liter and then convert this into cubic meters into cubic meters by multiplying by one meter for every 100 centimeters cubed, and we get 0.00175 cubic meters. So we add 62 kilograms to the mass of air in her lungs and then divide that by her volume that we calculated before, plus the volume of the air. This works out to 974 kilograms per cubic meter and that is less than the density of water and so yes, she will be able to float without treading water.