Question
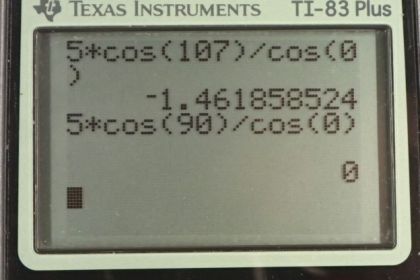
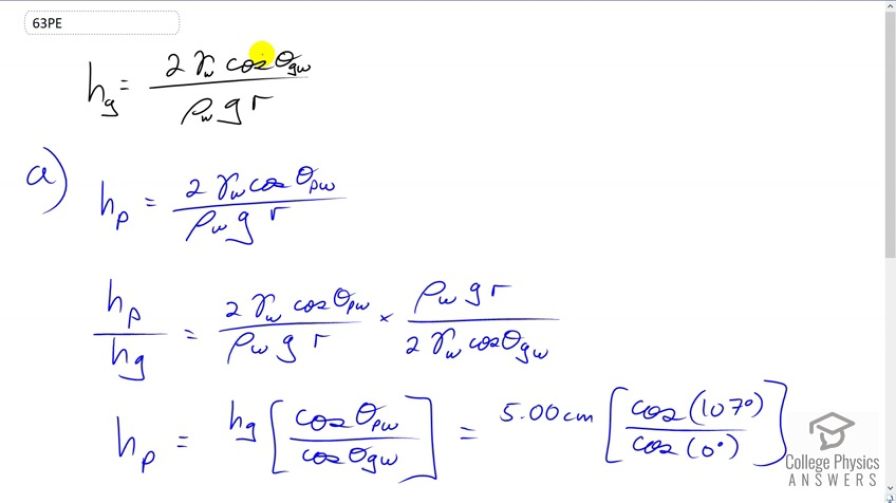
Suppose water is raised by capillary action to a height of 5.00 cm in a glass tube. (a) To what height will it be raised in a paraffin tube of the same radius? (b) In a silver tube of the same radius?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 63 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The height the water is raised up in a glass tube is two times the surface tension of water multiplied by cosine of the contact angle between glass and water, divided by the density of water times g times the radius of the tube that it's experiencing the capillary action in. So in paraffin wax, we have the same formula except there is a different contact angle but every other factor is the same, it's still water we're dealing with so we're still using the surface tension of water and the density of water. It's the same size tube we're told so the radius does not need a subscript. So let's take the ratio of these two heights and that's going to be this thing copied here, and then multiplied by the reciprocal of this instead of dividing by it because we don't want a fraction within a fraction since that looks difficult and complicated. So we're going to multiply by its reciprocal and we see that a lot of common factors cancel. We have all these things disappearing. There. We're left with the ratio of the angles, contact angles, is equal to the ratio of the heights. So we multiply both sides by the height in glass because we know what that is, and the height in paraffin wax can be the height in glass multiplied by cosine of the contact angle between water and paraffin, divided by the cosine of the contact angle between water and glass. So that's five centimeters height with glass, times cosine of 107 degrees over cos zero which is one, and that gives negative 1.46 centimeters. So this paraffin wax tube will actually push down the water in comparison to the water around it. So if you put a paraffin wax tube -- drawing in black here, and have the water level down here like this, it won't have a shape like that, I don't think anyway. So now in silver, a silver tube, we have the height in glass times cosine of the contact angle between water and silver, divided by cosine of the contact angle between water and glass. So we have five centimeters times cos 90 degrees over cos zero and that'll be zero. So there'd be no height raised at all.