Question
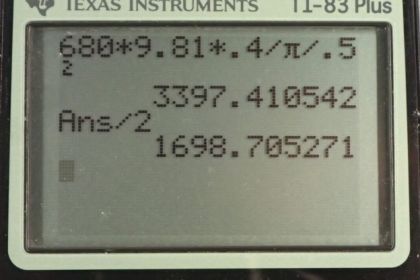
A cylindrical drum of radius 0.5 m is used to hold 400 liters of petroleum ether (density = .68 g/mL or ).
(Note: )
- Determine the amount of pressure applied to the walls of the drum if the petroleum ether fills the drum to its top.
- Determine the amount of pressure applied to the floor of the drum if the petroleum ether fills the drum to its top.
- If the drum were redesigned to hold 800 liters of petroleum ether:
- How would the pressure on the walls change? Would it increase, decrease, or stay the same?
- How would the pressure on the floor change? Would it increase, decrease, or stay the same?
Final Answer
- i) average pressure increases with increases in volume. ii) Pressure at the floor of the container increases with volume.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 5 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are asked to find the radius of this cylindrical column of coffee in a coffee cup. We're told the height is seven and a half centimeters and that the density of the coffee is the same as that of water. So it is one gram per milliliter which we convert into one gram per cubic centimeter in order to work with the centimeters given to us in the height. We're told the mass of the coffee is 375 grams. So the volume of the cylinder is the area of one end, pi r squared, multiplied by the height h. We can come up with another expression for volume in terms of the mass of the coffee. We'll say that the density of coffee is mass divided by its volume and we'll solve this for V by multiplying by V over rho on both sides. So we have V equals mass times density. So now we have two expressions for volume and so we can equate the two of them. So I'm substituting m rho in place of V here. So we have m rho equals pi r squared h and then we'll solve this for r. We'll divide both sides by pi times h and then switch the sides around to isolate r on the left or r squared anyhow, and then we'll take the square root of both sides. We get r equals square root of mass times density divided by pi times h. That's the square root of 375 grams times one gram per cubic centimeter divided by pi times seven and a half centimeters, giving us 3.99 centimeters. Most of the time in our formulas we convert our units into meters, kilograms, and seconds, mks units, but we did not do that here just because it's clear that they do work together anyway. We have grams together and we have centimeters. So as long as your units are consistent within a formula that's what's most important. We could have converted this into kilograms and the centimeters into meters but that would be unnecessary work in this case.