Question
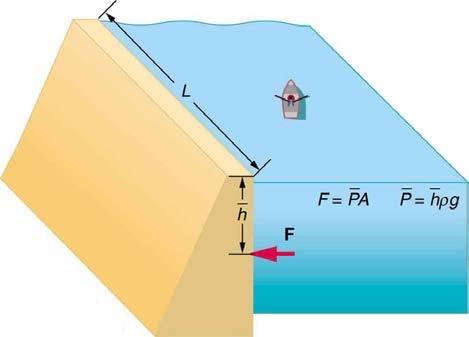
Show that the total force on a rectangular dam due to the water behind it increases with the square of the water depth. In particular, show that this force is given by , where is the density of water, is its depth at the dam, and is the length of the dam. You may assume the face of the dam is vertical. (Hint: Calculate the average pressure exerted and multiply this by the area in contact with the water. (See Figure 11.45.)
Final Answer
see video solution for derivation.
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 23 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job is to derive this expression for the force on a dam as a function of the height of the water behind it and the horizontal length of the dam as well. It shows that the pressure is proportional to the square of the height. Let's figure out why. So the average pressure because the pressure changes, here is zero at the very top and then here it's maximal pressure at the very bottom. Since that increases linearly with depth, linearly meaning it depends on the height to the power of one, we can get the average pressure by just taking the simple arithmetic average of the pressures at the top and the bottom. So that is zero plus rho g h at the bottom divided by two and this works out to rho g h over two. So now we'll say that the average pressure is the force that we're trying to find divided by the area of the surface of the dam in contact with the water. We can solve for F by multiplying both sides by A so it's average pressure multiplied by area. So that's rho g h over two multiplied by length times height, this is the area of the dam, and the h's get multiplied together to make h squared and we have the expression now, rho g hsquared l over two.