Question
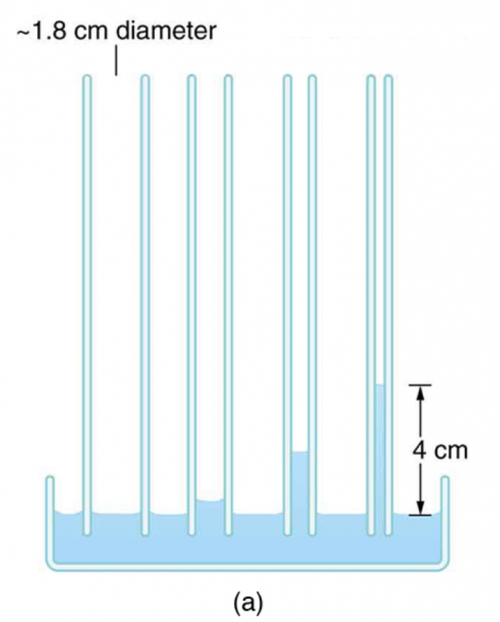
Figure 11.34(a) shows the effect of tube radius on the height to which capillary action can raise a fluid. (a) Calculate the height for water in a glass tube with a radius of 0.900 cm—a rather large tube like the one on the left. (b) What is the radius of the glass tube on the right if it raises water to 4.00 cm?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 11, Problem 58 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
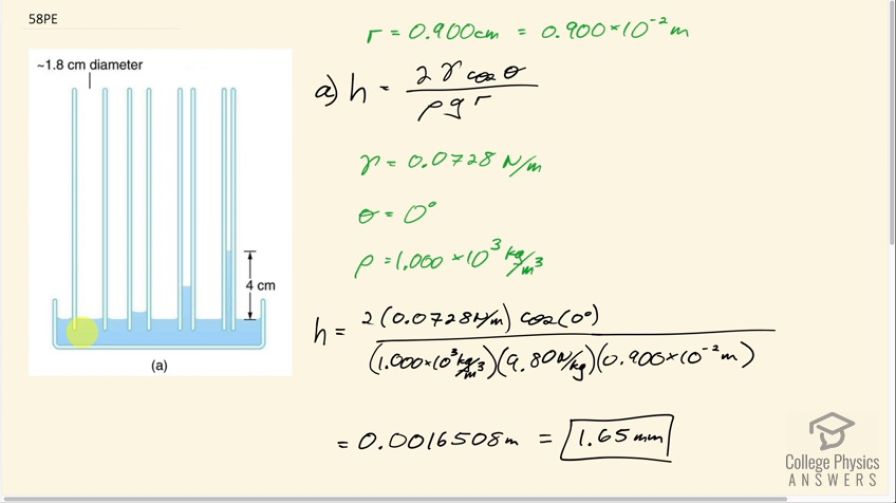
This is College Physics Answers with Shaun Dychko. A glass tube is placed in water and capillary action causes the water to go up inside the glass tube and it will go up this height h and that equals 2 times the surface tension of the fluid, which is water, times cosine of the contact angle between water and glass divided by density of water times gravitational field strength times the radius of the tube. So the radius of the tube is given to us as 0.900 centimeters and the prefix 'centa' means times 10 to the minus 2 so I convert that into meters and then we look up in our various data tables what each of these factors are: the γ, ρ and Θ. So for γ, the surface tension— that's table [11.3]— and the surface tension of water, we'll assume it's about 20 degrees so we will say 0.0728 newtons per meter and then the contact angle between water and glass is 0 degrees and then the density of water is 1.000 times 10 to the 3 kilograms per cubic meter. So the height that the water will go up then is 2 times 0.0728 newtons per meter times cos of 0 divided by the density of water times 9.80 newtons per kilogram times the radius of the tube and this gives us 1.65 millimeters of height. So it seems to be maybe kind of like this big tube here or maybe this one, goes up almost just an imperceptible amount compared to this 4.0 centimeters. Then in part (b), we are told that the water column in the tube is 4.0 centimeters in height, suppose, and then figure out what the radius would be to make that happen. So we are gonna rearrange this to solve for r by multiplying both sides by r over h and so we have the radius of the tube then is 2 times surface tension times cos of the contact angle divided by density times g times the height. So plug in all of our numbers including 4 times 10 to the minus 2 meters for the radius and we get 0.371 millimeters must be the radius of the glass tube.
