Question
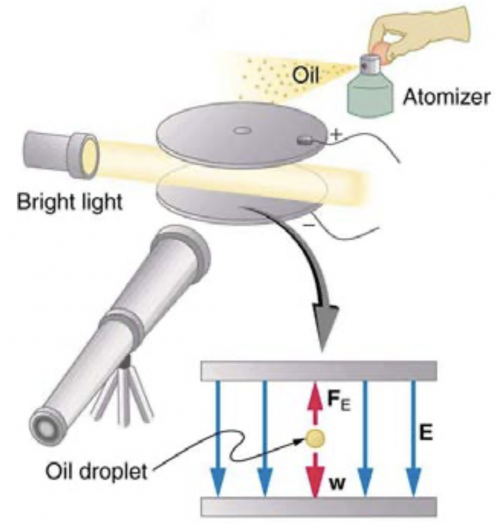
In a Millikan oil-drop experiment using a setup like that in Figure 30.9, a 500-V potential difference is applied to plates separated by 2.50 cm. (a) What is the mass of an oil drop having two extra electrons that is suspended motionless by the field between the plates? (b) What is the diameter of the drop, assuming it is a sphere with the density of olive oil?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 56 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
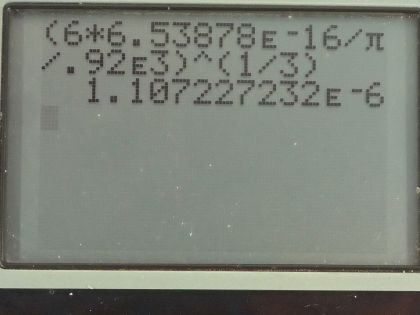
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Millikan Oil Drop experiment has a potential difference between these parallel plates of 500 volts and the separation between the plates is 2.50 centimeters so this distance here is d and the electric field strength then is this voltage divided by the separation between the plates and the force upwards due to the electric field then is the charge q times that electric field and the charge is 2 times the elementary charge since we are told there are 2 extra electrons on an oil drop and so that's 2 times 1.602 times 10 to the minus 19 coulombs for a total of this much charge. So that charge times the electric field equals the weight downwards, which is the mass times gravitational field strength downwards. Now electric field we'll substitute with voltage divided by separation between plates and then we can solve this for m—the mass— by dividing both sides by g. So the mass then is the charge times the voltage divided by gravitational field strength times separation between the plates. So that's 3.204 times 10 to the minus 19 coulombs times 500 volts divided by 9.80 newtons per kilogram times 2.50 times 10 to the minus 2 meters and this works out to 6.54 times 10 to the minus 16 kilograms. Now in part (b), we are asked what is the diameter of the drop assuming it's a sphere and it has the same density as olive oil? Well, we need to look at table [11.1] to find the density of olive oil— that's 0.92 times 10 to the 3 kilograms per cubic meter— and that density is the drop's mass divided by its volume its volume is four-thirds πr cubed where we can substitute diameter divided by 2 in place of r and then cube d over 2 to get cubed d over 8 and then 4 over 8 makes a half at the bottom times a 3 in the bottom makes 6 in the denominator so that's πd cubed over 6 is going to be our formula for volume. Now we are dividing by this fraction so we'll instead multiply by its reciprocal so we'll flip it over and multiply m by it so m is going to be multiplied by 6 over πd cubed and then we can solve for d cubed by multiplying both sides by d cubed over ρ and then we get diameter cubed is 6m over πρ and then we take the cube root of both sides and the cube root by the way is the same as the exponent one-third, which is how I am going to plug it into my calculator so this is exponent one-third. So the diameter of the drop then is 6 times the mass that we calculated in part (a) divided by π times the density of olive oil all to the power of one-third and that is 1.11 micrometers.