Question
An electron in a hydrogen atom is initially in energy level 2 (). (a) What frequency of photon must be absorbed by the atom in order for the electron to transition to energy level 3 ()? (b) What frequency of photon must be emitted by the atom in order for the electron to transition to energy level 1 ()?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 6 (Test Prep for AP® Courses)
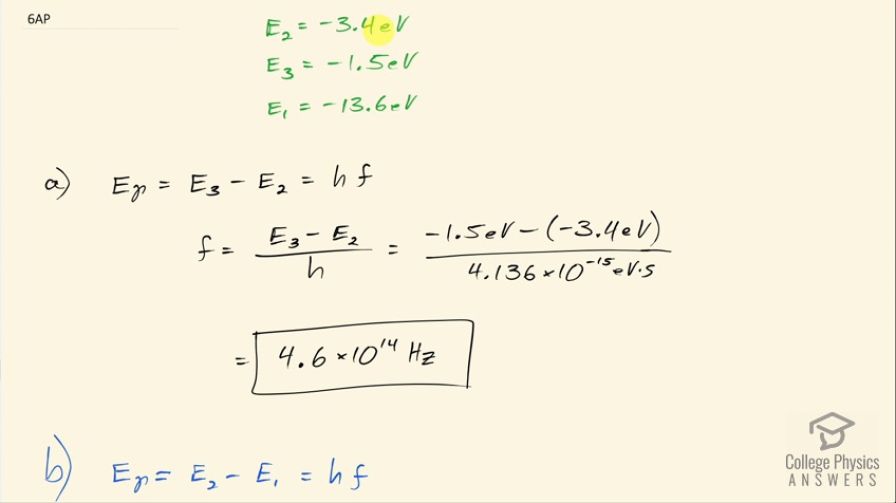
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An electron in hydrogen starts at an energy level of 2 which has an energy of negative 3.4 electron volts and the question is what frequency of photon must be absorbed in order for the electron to transition up to energy level 3 that has an energy of negative 1.5 electron volts? So the photon energy has to be equal to the difference in these two energy levels and the energy of the photon is Planck's constant multiplied by frequency and so we can divide both sides by Planck's constant to solve for f here and so the frequency of the photon then is the difference between the energy levels divided by Planck's constant. So that's negative 1.5 electron volts for the final energy level minus negative 3.4 electron volts for the initial energy level divided by Planck's constant written with units of electron volt seconds so that our units in the end are reciprocal seconds, which is abbreviated with hertz and so we have 4.6 times 10 to the 14 hertz. And then in part (b) it's asking what frequency of photon will be emitted by the atom in order for the electron to transition to energy level 1? So the energy of the photon emitted will be equal to the difference between energy levels 2 and 1 and so we can solve for the frequency again by dividing both sides by Planck's constant. So the frequency will be negative 3.4 electron volts—where it starts— minus negative 13.6 electron volts— energy where it ends— divided by 4.136 times 10 to the minus 15 electron volt seconds and we get 2.5 times 10 to the 15 hertz.
