(a) Calculate the magnitude of the angular momentum for an $l=1$ electron. (b) Compare your answer to the value Bohr proposed for the $n=1$ state.

Video Transcript

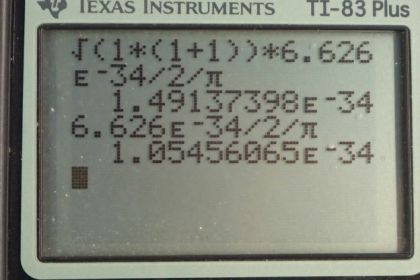
This is College Physics Answers with Shaun Dychko. The magnitude of the angular momentum for an electron with an angular momentum quantum number of 1 is given by square root of l times l plus 1 times Planck's constant divided by 2π. So that's the square root of 1 times 2 times 6.626 times 10 to the minus 34 joule seconds—Planck's constant— divided by 2π which is 1.49 times 10 to the minus 34 joule seconds. Now Bohr in equation [30.20] created a different expression for the magnitude of the angular momentum based on assumptions about circular orbits and he said that it's the principal quantum number multiplied by h over 2π. So in this case, n is 1. Why is it 1? Oh yeah because as the question says suppose it's 1. Alright. Good. Sorry about that. And it's 1.05 times 10 to the minus 34 joule seconds. So at least they have the same order of magnitude and so that's pretty close enough considering he's made some some major assumptions about circular orbits which we now know are not even remotely true because orbits can be very strangely shaped; they can even be barbell shaped for a p orbit and so on.