Question
An atom has an electron with . What is the smallest value of for this electron?
Final Answer
3
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 36 (Problems & Exercises)
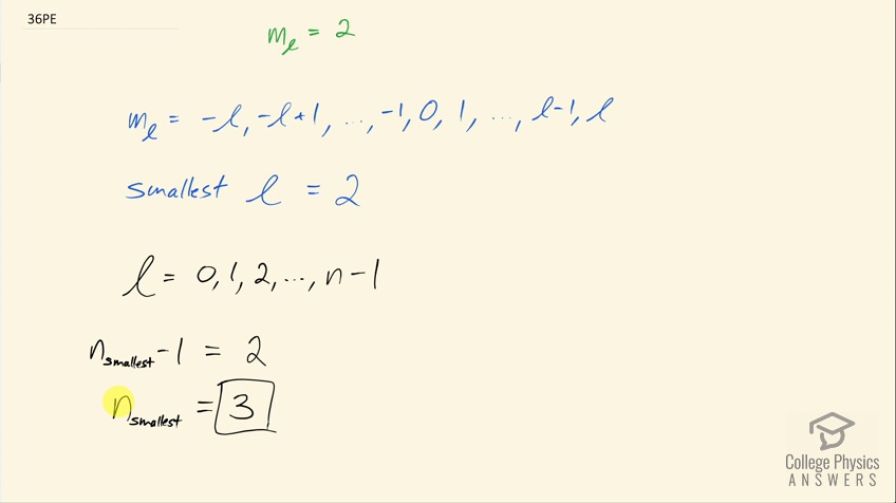
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told that the angular momentum projection number is 2 and we are asked to figure out what is the smallest possible value for the principal quantum number n? Now we know that n is related to the angular momentum quantum number by this sequence here l goes from 0 up to n minus 1 in integers or whole numbers I guess you should say and so if we can minimize l then we'll minimize n and so we look at this sequence here for the possible values for the angular momentum projection number to figure out what the smallest possible value for l is. So we know m l is 2—that's for sure— now l can be 2, it cannot be 1 because the maximum possible value for m l is l and so given that m l is 2; l cannot be 1 since that would be less than 2; l could be 3 in which case 2 is allowed for m l because you can have 3 minus 1 to make 2 but we have to minimize l with the smallest possible 1 and the smallest possible number for l is 2 because that works because m l can be l itself. Okay! So 2 is the smallest value for the angular momentum quantum number. So the angular momentum quantum number goes from 0 all the way up to n minus 1 and so we can say n minus 1 at its smallest is going to be 2 in which case the smallest principal quantum number then is 3.