Question
Atoms can be ionized by thermal collisions, such as at the high temperatures found in the solar corona. One such ion is
, a carbon atom with only a single electron.
(a) By what factor are the energies of its hydrogen-like levels
greater than those of hydrogen?
(b) What is the wavelength of the first line in this ion’s Paschen series?
(c) What type of EM radiation is this?
Final Answer
- The orbital energies of are greater than those of hydrogen by a factor of
- This is ultraviolet radiation.
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 22 (Problems & Exercises)
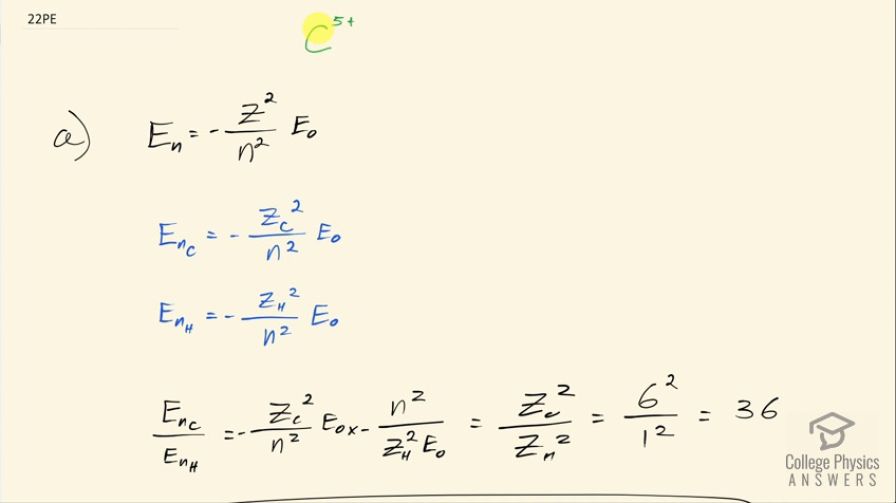
vote with a rating of
votes with an average rating of
.
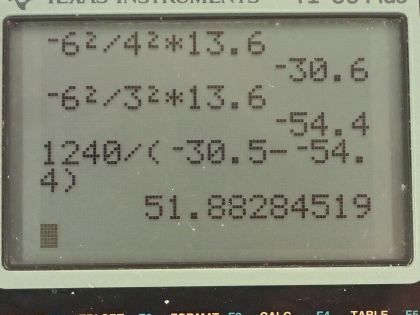
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Carbon atoms get ionized in the solar corona by the collisions between different carbon atoms and they might lose five of their electrons leaving only one electron surrounding this nucleus that has six protons. The question in part (a) is by what factor do the energies of its hydrogen like levels differ from those of hydrogen? The orbital energy of the nth orbital is equal to the negative of the number of protons in the nucleus squared divided by the energy level squared multiplied by this ground state energy for an electron in hydrogen. So the nth level for carbon is the number of protons in carbon squared over n squared times E naught and whereas for hydrogen, the only difference between these two formulas is that we have the number of protons in a hydrogen nucleus. So when we divide these two, we take the energy for carbon and then multiply it by the reciprocal of the energy for hydrogen and the negatives cancel and the n squared's cancel and the E naught cancels so we are left with Z C squared over Z H squared and that equals 6 squared over 1 squared and that is 36. So the orbital energies of the C 5+ ion are greater than those of hydrogen by a factor of 36. And in part (b) we are asked what is the wavelength of the first line in this ion's Paschen series? So the Paschen series means that the electron ends at the 3rd orbital or the 3rd principal quantum number and the first wavelength or first line in this ion's Paschen series— the lowest energy 1— will have a starting level of 4. Now we need to figure out what the energy difference is between these two levels at n equals 4 and n equals 3 and that energy difference will be the energy of the photon that is emitted and that will be Planck's constant times its frequency. Now from the wave equation we can figure out what the frequency is in terms of wavelength and we divide both sides by λ here and we say that frequency is the speed of light divided by the wavelength and we plug that in for f here and then solve for λ by multiplying both sides by λ divided by the change in energy as the electron transitions from the fourth orbital to the third so the wavelength then is hc over the difference in energy levels. So the energy level for carbon— I am just repeating the formula that I had up above there— so that's going to be 6 squared divided by 4 squared and that's negative times 13.6 electron volts— that's the ground state energy for the electron in hydrogen atom— that is negative 30.6 electron volts. And then it goes down to the third energy level so that's going to be negative 6 squared over 3 squared times 13.6 electron volts and that's negative 54.4 electron volts. So the wavelength emitted then is 1240 electron volt nanometers where I have taken this convenient number in place of hc and it's convenient because it has units of electron volts which will cancel with the electron volts in the denominator and leaving us with units of nanometers for our length of the wavelength. So we are dividing that by negative 30.6 electron volts minus negative 54.4 electron volts and that is 51.9 nanometers. Ultraviolet light has a wavelength between 10 nanometers and 380 nanometers and this falls within that range so the wavelength emitted in the first line in the Paschen series is ultraviolet radiation.