Question
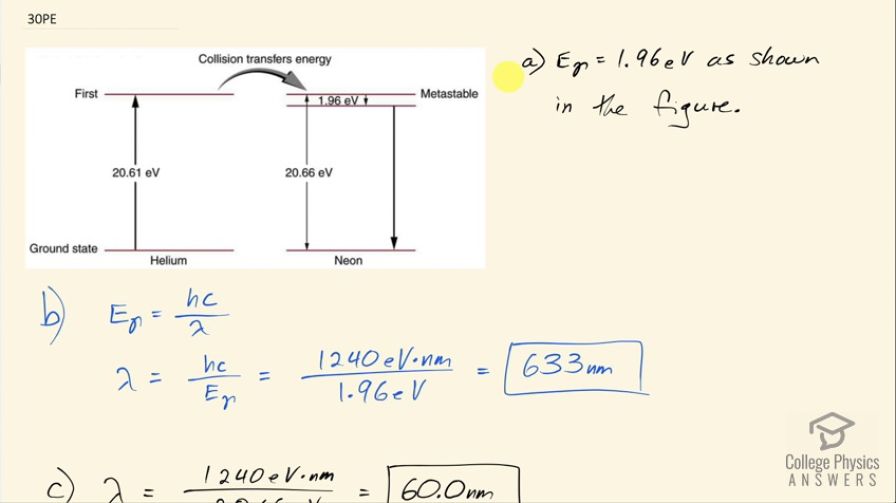
Figure 30.39 shows the energy-level diagram for neon. (a) Verify that the energy of the photon emitted when neon goes from its metastable state to the one immediately below is equal to 1.96 eV. (b) Show that the wavelength of this radiation is 633 nm. (c) What wavelength is emitted when the neon makes a direct transition to its ground state?
<b>Figure 30.39</b>Energy levels in helium and neon. In the common helium-neon laser, an electrical discharge pumps energy into the metastable states of both atoms. The gas mixture has about ten times more helium atoms than neon atoms. Excited helium atoms easily de-excite by transferring energy to neon in a collision. A population inversion in neon is achieved, allowing lasing by the neon to occur.
Figure 30.39Energy levels in helium and neon. In the common helium-neon laser, an electrical discharge pumps energy into the metastable states of both atoms. The gas mixture has about ten times more helium atoms than neon atoms. Excited helium atoms easily de-excite by transferring energy to neon in a collision. A population inversion in neon is achieved, allowing lasing by the neon to occur.
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 1.96 eV1.96\textrm{ eV} is shown in the figure.
  2. 633 nm633 \textrm{ nm}
  3. 60.0 nm60.0\textrm{ nm}

Solution video

OpenStax College Physics for AP® Courses, Chapter 30, Problem 30 (Problems & Exercises)

OpenStax College Physics, Chapter 30, Problem 30 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 30, Problem 30 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. This is figure [30.39] and it shows the energy levels for neon and question (a) is asking us to verify that the energy of the photon emitted when neon goes from its metastable state to the one immediately below it that it will emit a photon with an energy of 1.96 electron volts but that's shown in the figure I mean the energy of the photon that gets emitted here... the photon will have an energy equal to the difference between these energy levels. Okay! So part (b) asks what is the wavelength of that photon? Well the energy of the photon is Planck's constant times speed of light divided by the wavelength and we can solve for λ by multiplying both sides by λ over the energy and I put the subscript λ on there just to say this is the energy of a photon. So the wavelength then is 1240 electron volt nanometers where I am choosing these convenient units for hc because the electron volts will cancel with the 1.96 electron volts in the denominator and we end up with an answer in nanometers, this works out to 633 nanometers and this is red light and this is the visible light that you see from a helium-neon laser. Part (c) asks for the wavelength of the photon emitted from a direct transition between this metastable state all the way to the ground state so that photon will have an energy equal to 20.66 electron volts. So we take 1240 electron volt nanometers divided by 20.66 electron volts and that is 60.0 nanometers— this is ultraviolet light.