Question
The maximum characteristic x-ray photon energy comes from the capture of a free electron into a shell vacancy. What is this photon energy in keV for tungsten, assuming the free electron has no initial kinetic energy?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
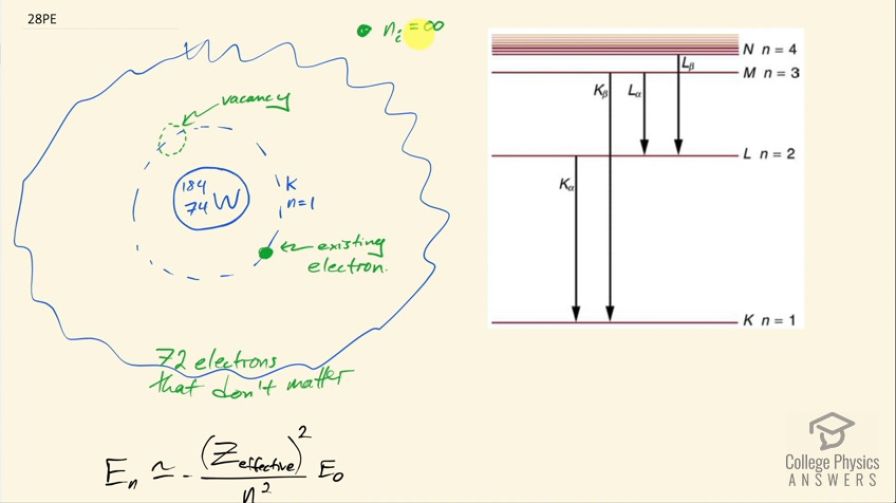
This is College Physics Answers with Shaun Dychko. An electron is beginning at an energy level of infinity so it's a free electron in other words and it's going to fill a vacancy in the k level of this tungsten ion and k corresponds to n equals 1 so it's the innermost energy level is the destination for this electron. Now at this innermost energy level, the other electrons in this ion don't matter because it's similar to a conductor that's surrounded by charge all around it and that charge is evenly distributed all around and the charges will cancel each other out in the interior of this conductor, there will be no electric field due to these charges inside the conductor; in a sense, it would be the same picture as if there were no charges at all inside the conductor... there's no electric field in either case. So that means we can ignore all these surrounding electrons of this tungsten ion and what that means is that this is similar to a hydrogen like ion or hydrogen like atom in that there's just essentially one electron involved and the other electrons don't matter except for this one, this one does matter and its effect is to make the nucleus seem as though it has a charge of only 73 protons. So we'll take the 74 protons that are in the tungsten nucleus, subtract 1 due to it being compensated for by this existing electron in the n equals 1 energy level and we'll use this formula to calculate the energy of this position based on an effective number of protons, which is 73. Okay! So the energy of the photon that will be emitted by this transition from n equals infinity to n equals 1 is going to be the negative of the difference in energy of the electron and that's the negative of its final energy state minus its initial energy state; initial energy state is 0 because that's defined to be a free electron has energy of zero and then the final energy state will be negative of this effective number of protons squared over the energy number principal quantum number squared, which is n and multiply by this ground state energy for hydrogen. So we have negative of negative 73 squared over 1 squared times 13.6 electron volts and that is 72.5 kiloelectron volts will be the energy of the photon emitted.
