Question
What are the approximate energies of the and x-rays for copper?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 29 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
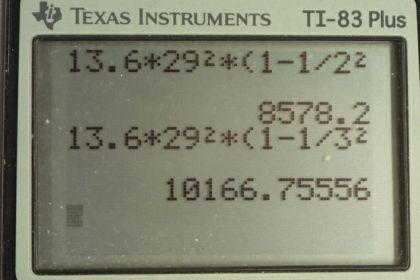
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to find the energies of some of the characteristic x-rays when copper is the anode at the end of an x-ray tube. So this picture tells us what the K α and K β transitions mean; these are old-fashioned labels for transitions between energy states where the final energy state is 1 and the initial energy state is n equals 2 for a K α transition and the initial energy state is n equals 3 for a K β transition. So the energy of any particular level is negative of the atomic number squared divided by the principal quantum number squared times the ground state energy which we take to be 13.6 electron volts for E naught. And to find the energy of the x-ray then we are going to find the difference between the initial energy of the electron minus the final energy. And so we use this formula twice substituting in different numbers for n each time. So we have negative 13.6 electron volts times Z squared over n i squared minus negative 13.6 electron volts times Z squared over n f squared and this 13.6 and this Z squared can be factored out. So the energy of the x-ray then is gonna be 13.6 electron volts times the number of protons squared times 1 over the final principal quantum number squared minus the 1 over the initial principal quantum number squared. So for a K α transition, n f is 1 and n i is 2 and so the energy of the x-ray for a K α transition will be 13.6 times 29 squared and 29 is the atomic number for copper— it's the number of protons in copper— and then we multiply that by 1 over 1 squared— the final principal quantum number— minus 1 over 2 squared giving 8.58 kiloelectron volts. And for the K β transition, n i is 3 and n f is 1 and so the energy for the x-ray in a K β transition is 13.6 electron volts times 29 squared times 1 over 1 squared minus 1 over 3 squared and that is 10.2 kiloelectron volts.