Using the given charge-to-mass ratios for electrons and protons, and knowing the magnitudes of their charges are equal, what is the ratio of the proton’s mass to the electron’s? (Note that since the charge-to-mass ratios are given to only three-digit accuracy, your answer may differ from the accepted ratio in the fourth digit.)

(a) Calculate the mass of a proton using the charge-to- mass ratio given for it in this chapter and its known charge. (b) How does your result compare with the proton mass given in this chapter?

If someone wanted to build a scale model of the atom with a nucleus 1.00 m in diameter, how far away would the nearest electron need to be?

Rutherford found the size of the nucleus to be about $10^{-15}\textrm{ m}$ . This implied a huge density. What would this density be for gold?

In Millikan’s oil-drop experiment, one looks at a small oil drop held motionless between two plates. Take the voltage between the plates to be 2033 V, and the plate separation to be 2.00 cm. The oil drop (of density $0.81 \textrm{ g/cm}^3$) has a diameter of $4.0 \times 10^{-6} \textrm{ m}$ . Find the charge on the drop, in terms of electron units.

(a) An aspiring physicist wants to build a scale model of a hydrogen atom for her science fair project. If the atom is 1.00 m in diameter, how big should she try to make the nucleus? (b) How easy will this be to do?

By calculating its wavelength, show that the first line in the Lyman series is UV radiation.

Find the wavelength of the third line in the Lyman series, and identify the type of EM radiation.

Look up the values of the quantities in $a_B = \dfrac{h^2}{4\pi^2m_ekq_e^2}$, and verify that the Bohr radius $a_B$ is $0.529\times 10^{-10}\textrm{ m}$.

Verify that the ground state energy $E_0$ is $13.6\textrm{ eV}$ by using $E_0 = \dfrac{2 \pi^2 q_e^4 m_e k^2}{h^2}$.

If a hydrogen atom has its electron in the $n = 4$ state, how much energy in eV is needed to ionize it?

A hydrogen atom in an excited state can be ionized with less energy than when it is in its ground state. What is $n$ for a hydrogen atom if 0.850 eV of energy can ionize it?

Find the radius of a hydrogen atom in the $n = 2$ state according to Bohr’s theory.

Show that $\dfrac{13.6\textrm{ eV}}{hc} = 1.097\times 10^{7}\textrm{ /m} = R$ (Rydberg's constant), as discussed in the text.

What is the smallest-wavelength line in the Balmer series? Is it in the visible part of the spectrum?

Show that the entire Paschen series is in the infrared part of the spectrum. To do this, you only need to calculate the shortest wavelength in the series.

Do the Balmer and Lyman series overlap? To answer this, calculate the shortest-wavelength Balmer line and the longest-wavelength Lyman line.

(a) Which line in the Balmer series is the first one in the UV part of the spectrum? (b) How many Balmer series lines are in the visible part of the spectrum? (c) How many are in the UV?

A wavelength of $4.653\textrm{ }\mu\textrm{m}$ is observed in a hydrogen spectrum for a transition that ends in the $n_f = 5$ level. What was $n_i$ for the initial level of the electron?

A singly ionized helium ion has only one electron and is denoted $\textrm{He}^+$ . What is the ion’s radius in the ground state compared to the Bohr radius of hydrogen atom?

A beryllium ion with a single electron (denoted $Be^{3+} ) is in an excited state with radius the same as that of the ground state of hydrogen.

1. What is $n$ for the $Be^{3+}$ ion?
2. How much energy in eV is needed to ionize the ion from this excited state?

Atoms can be ionized by thermal collisions, such as at the high temperatures found in the solar corona. One such ion is $\textrm{C}^{+5}$, a carbon atom with only a single electron. (a) By what factor are the energies of its hydrogen-like levels greater than those of hydrogen? (b) What is the wavelength of the first line in this ion’s Paschen series? (c) What type of EM radiation is this?

Verify equations $r_n = \dfrac{n^2}{Z}a_B$ and $a_B = \dfrac{h^2}{4\pi^2m_ekq_e^2} = 0.529 \times 10^{-10}\textrm{ m}$ using the approach stated in the text. That is, equate the Coulomb and centripetal forces and then insert an expression for velocity from the condition for angular momentum quantization.

The wavelength of the four Balmer series lines for hydrogen are found to be 410.3, 434.2, 486.3, and 656.5 nm. What average percentage difference is found between these wavelength numbers and those predicted by $\dfrac{1}{\lambda} = R \left ( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right )$? It is amazing how well a simple formula (disconnected originally from theory) could duplicate this phenomenon.

(a) What is the shortest-wavelength x-ray radiation that can be generated in an x-ray tube with an applied voltage of 50.0 kV? (b) Calculate the photon energy in eV. (c) Explain the relationship of the photon energy to the applied voltage.

A color television tube also generates some x rays when its electron beam strikes the screen. What is the shortest wavelength of these x rays, if a 30.0-kV potential is used to accelerate the electrons? (Note that TVs have shielding to prevent these x rays from exposing viewers.)

An x ray tube has an applied voltage of 100 kV. (a) What is the most energetic x-ray photon it can produce? Express your answer in electron volts and joules. (b) Find the wavelength of such an X–ray.

The maximum characteristic x-ray photon energy comes from the capture of a free electron into a $K$ shell vacancy. What is this photon energy in keV for tungsten, assuming the free electron has no initial kinetic energy?

What are the approximate energies of the $K_{\alpha}$ and $K_{\beta}$ x-rays for copper?

Figure 30.39 shows the energy-level diagram for neon. (a) Verify that the energy of the photon emitted when neon goes from its metastable state to the one immediately below is equal to 1.96 eV. (b) Show that the wavelength of this radiation is 633 nm. (c) What wavelength is emitted when the neon makes a direct transition to its ground state?

A helium-neon laser is pumped by electric discharge. What wavelength electromagnetic radiation would be needed to pump it? See Figure 30.39 for energy-level information.

Ruby lasers have chromium atoms doped in an aluminum oxide crystal. The energy level diagram for chromium in a ruby is shown in Figure 30.64. What wavelength is emitted by a ruby laser?

(a) What energy photons can pump chromium atoms in a ruby laser from the ground state to its second and third excited states? (b) What are the wavelengths of these photons? Verify that they are in the visible part of the spectrum.

Some of the most powerful lasers are based on the energy levels of neodymium in solids, such as glass, as shown in Figure 30.65. (a) What average wavelength light can pump the neodymium into the levels above its metastable state? (b) Verify that the 1.17 eV transition produces $1.06\textrm{ }\mu\textrm{m}$ radiation.

If an atom has an electron in the $n = 5$ state with $m_l = 3$ , what are the possible values of $l$?

An atom has an electron with $m_l = 2$ . What is the smallest value of $n$ for this electron?

What are the possible values of $m_l$ for an electron in the $n = 4$ state?

What, if any, constraints does a value of $m_l = 1$ place on the other quantum numbers for an electron in an atom?

(a) Calculate the magnitude of the angular momentum for an $l = 1$ electron. (b) Compare your answer to the value Bohr proposed for the $n = 1$ state.

(a) What is the magnitude of the angular momentum for an $l=1$ electron? (b) Calculate the magnitude of the electron’s spin angular momentum. (c) What is the ratio of these angular momenta?

(a) What is the magnitude of the angular momentum for an $l = 3$ electron? (b) Calculate the magnitude of the electron’s spin angular momentum. (c) What is the ratio of these angular momenta?

(a) How many angles can $L$ make with the z -axis for an $l = 2$ electron? (b) Calculate the value of the smallest angle.

What angles can the spin $S$ of an electron make with the z -axis?

(a) What is the minimum value of $l$ for a subshell that has 11 electrons in it? (b) If this subshell is in the $n = 5$ shell, what is the spectroscopic notation for this atom?

(a) List all possible sets of quantum numbers $\left ( n, l, m , m_s \right )$ for the $n = 3$ shell, and determine the number of electrons that can be in the shell and each of its subshells. (b) Show that the number of electrons in the shell equals $2n^2$ and that the number in each subshell is $2(2l + 1)$.

Which of the following spectroscopic notations are not allowed? (a) $5s^1$ (b) $1d^1$ (c) $4s^3$ (d) $3p^7$ (e) $5g^{15}$. State which rule is violated for each that is not allowed.

Which of the following spectroscopic notations are allowed (that is, which violate none of the rules regarding values of quantum numbers)?

1. $1s^1$
2. $1d^3$
3. $4s^2$
4. $3p^7$
5. $6h^{20}$

(a) Using the Pauli exclusion principle and the rules relating the allowed values of the quantum numbers $(n, l, m_l, m_s)$, prove that the maximum number of electrons in a subshell is $2(2l+1)$. (b) In a similar manner, prove that the maximum number of electrons in a shell is $2n^2$.

Estimate the density of a nucleus by calculating the density of a proton, taking it to be a sphere 1.2 fm in diameter. Compare your result with the value estimated in this chapter.

The electric and magnetic forces on an electron in the CRT in Figure 30.7 are supposed to be in opposite directions. Verify this by determining the direction of each force for the situation shown. Explain how you obtain the directions (that is, identify the rules used).

(a) What is the distance between the slits of a diffraction grating that produces a first-order maximum for the first Balmer line at an angle of $20.0^\circ$? (b) At what angle will the fourth line of the Balmer series appear in first order? (c) At what angle will the second-order maximum be for the first line?

A galaxy moving away from the earth has a speed of $0.0100c$ . What wavelength do we observe for an $n_i = 7$ to $n_f = 2$ transition for hydrogen in that galaxy?

Calculate the velocity of a star moving relative to the earth if you observe a wavelength of 91.0 nm for ionized hydrogen capturing an electron directly into the lowest orbital (that is, a $n_i = \infty$ to $n_f = 1$, or a Lyman series transition).

In a Millikan oil-drop experiment using a setup like that in Figure 30.9, a 500-V potential difference is applied to plates separated by 2.50 cm. (a) What is the mass of an oil drop having two extra electrons that is suspended motionless by the field between the plates? (b) What is the diameter of the drop, assuming it is a sphere with the density of olive oil?

What double-slit separation would produce a first-order maximum at $3.00^\circ$ for 25.0-keV x rays? The small answer indicates that the wave character of x rays is best determined by having them interact with very small objects such as atoms and molecules.

In a laboratory experiment designed to duplicate Thomson’s determination of $\dfrac{q_e}{m_e}$ , a beam of electrons having a velocity of $6.00\times 10^{7}\textrm{ m/s}$ enters a $5.00\times 10^{-3}\textrm{ T}$ magnetic field. The beam moves perpendicular to the field in a path having a 6.80-cm radius of curvature. Determine $\dfrac{q_e}{m_e}$ from these observations, and compare the result with the known value.

Find the value of $l$, the orbital angular momentum quantum number, for the moon around the earth. The extremely large value obtained implies that it is impossible to tell the difference between adjacent quantized orbits for macroscopic objects.

Particles called muons exist in cosmic rays and can be created in particle accelerators. Muons are very similar to electrons, having the same charge and spin, but they have a mass 207 times greater. When muons are captured by an atom, they orbit just like an electron but with a smaller radius, since the mass in $a_\textrm{B} = \dfrac{h^2}{4\pi^2m_ekq_e^2} = 0.529\times 10^{-10}\textrm{ m}$ is $207m_e$. (a) Calculate the radius of the $n=1$ orbit for a muon in a uranium ion ($Z = 92$). (b) Compare this with the 7.5-fm radius of a uranium nucleus. Note that since the muon orbits inside the electron, it falls into a hydrogen-like orbit. Since your answer is less than the radius of the nucleus, you can see that the photons emitted as the muon falls into its lowest orbit can give information about the nucleus.

Calculate the minimum amount of energy in joules needed to create a population inversion in a helium-neon laser containing $1.00\times 10^{-4}\textrm{ mols}$ of neon.

A carbon dioxide laser used in surgery emits infrared radiation with a wavelength of $10.6\textrm{ }\mu\textrm{m}$. In $1.00\textrm{ ms}$ this laser raised the temperature of $1.00\textrm{ cm}^3$ of flesh to $100^\circ\textrm{C}$ and evaporated it. (a) How many photons were required? You may assume flesh has the same heat of vaporization as water. (b) What was the minimum power output during the flash?

Suppose an MRI scanner uses 100-MHz radio waves. (a) Calculate the photon energy. (b) How does this compare to typical molecular binding energies?

(a) An excimer laser used for vision correction emits 193-nm UV. Calculate the photon energy in eV. (b) These photons are used to evaporate corneal tissue, which is very similar to water in its properties. Calculate the amount of energy needed per molecule of water to make the phase change from liquid to gas. That is, divide the heat of vaporization in kJ/kg by the number of water molecules in a kilogram. (c) Convert this to eV and compare to the photon energy. Discuss the implications.

A neighboring galaxy rotates on its axis so that stars on one side move toward us as fast as 200 km/s, while those on the other side move away as fast as 200 km/s. This causes the EM radiation we receive to be Doppler shifted by velocities over the entire range of ±200 km/s. What range of wavelengths will we observe for the 656.0-nm line in the Balmer series of hydrogen emitted by stars in this galaxy. (This is called line broadening.)

A pulsar is a rapidly spinning remnant of a supernova. It rotates on its axis, sweeping hydrogen along with it so that hydrogen on one side moves toward us as fast as 50.0 km/s, while that on the other side moves away as fast as 50.0 km/s. This means that the EM radiation we receive will be Doppler shifted over a range of $\pm 50.0\textrm{ km/s}$. What range of wavelengths will we observe for the 91.20-nm line in the Lyman series of hydrogen? (Such line broadening is observed and actually provides part of the evidence for rapid rotation.)

Prove that the velocity of charged particles moving along a straight path through perpendicular electric and magnetic fields is $v = \dfrac{\textrm{E}}{\textrm{B}}$ . Thus crossed electric and magnetic fields can be used as a velocity selector independent of the charge and mass of the particle involved.

(a) What voltage must be applied to an X-ray tube to obtain 0.0100-fm-wavelength X-rays for use in exploring the details of nuclei? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

A student in a physics laboratory observes a hydrogen spectrum with a diffraction grating for the purpose of measuring the wavelengths of the emitted radiation. In the spectrum, she observes a yellow line and finds its wavelength to be 589 nm. (a) Assuming this is part of the Balmer series, determine $n_i$ , the principal quantum number of the initial state. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

In an experiment, three microscopic latex spheres are sprayed into a chamber and become charged with +3e, +5e, and −3e, respectively. Later, all three spheres collide simultaneously and then separate. Which of the following are possible values for the final charges on the spheres? Select two answers.

1. $+4e, -4e, +5e$
2. $-4e, +4.5e, +4.5e$
3. $+5e, -8e, +7e$
4. $+6e, +6e, -7e$

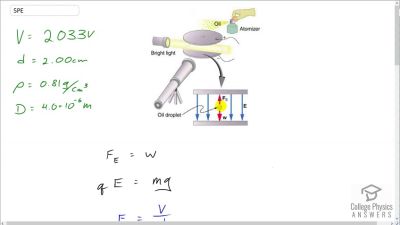
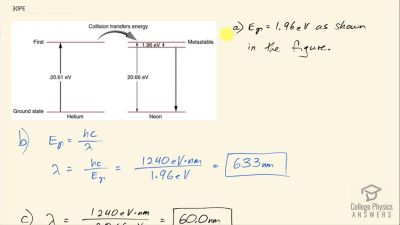
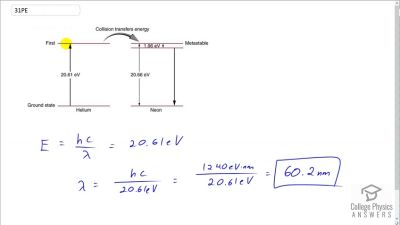
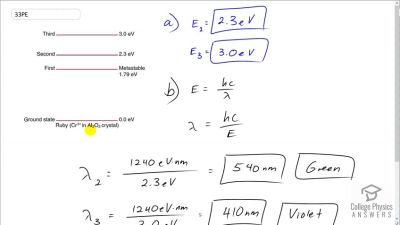
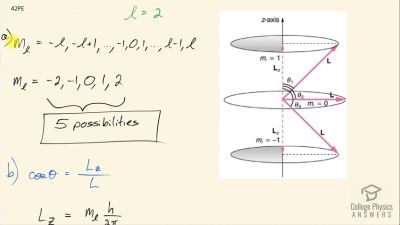
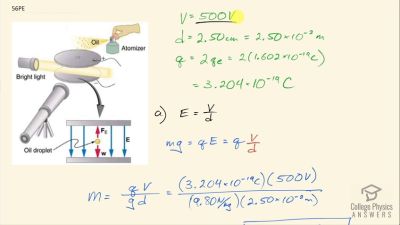
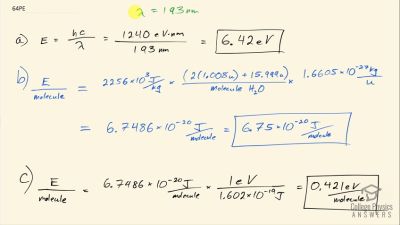
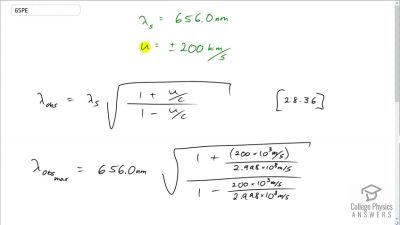
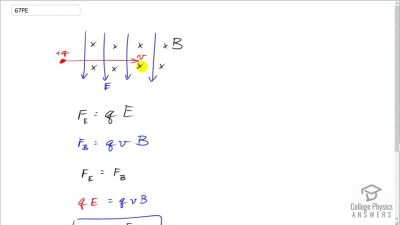
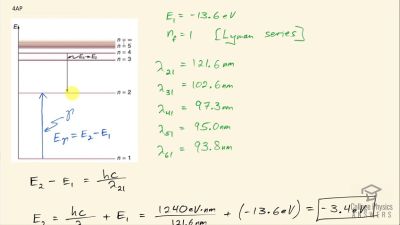
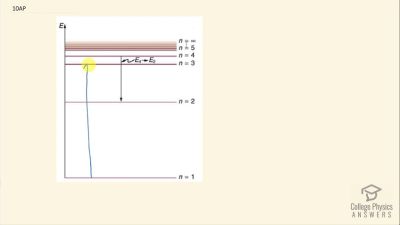
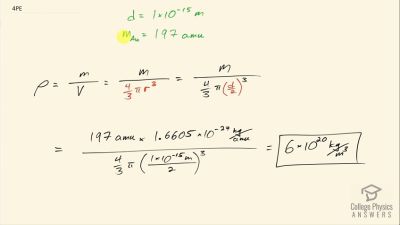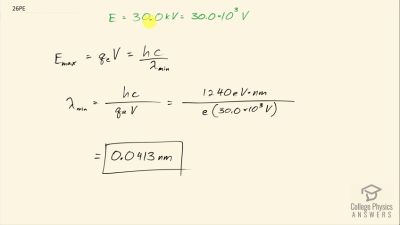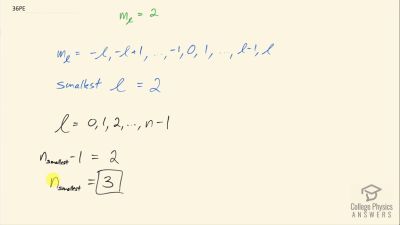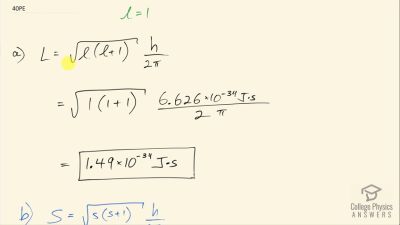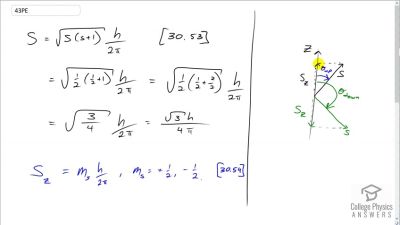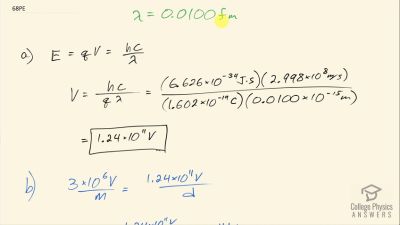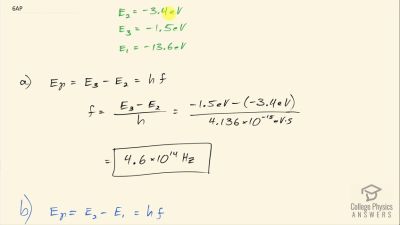In Millikan’s oil drop experiment, he experimented with various voltage differences between two plates to determine what voltage was necessary to hold a drop motionless. He deduced that the charge on the oil drop could be found by setting the gravitational force on the drop (pointing downward) equal to the electric force (pointing upward): $m_\textrm{drop}g = qE$ , where $m_\textrm{drop}$ is the mass of the oil drop, $g$ is the gravitational acceleration ($9.8\textrm{ m/s}^2$ ), $q$ is the net charge of the oil drop, and $E$ is the electric field between the plates. Millikan deduced that the charge on an electron, $e$, is $1.6\times 10^{-19}\textrm{ C}$. For a system of oil drops of equal mass ($1.0\times 10^{-15}\textrm{ kilograms}$), describe what value or values of the electric field would hold the drops motionless.

A hypothetical one-electron atom in its highest excited state can only emit photons of energy $2E, 3E$, and $5E$ before reaching the ground state. Which of the following represents the complete set of energy levels for this atom?

1. $0, 3E, 5E$
2. $0, 2E, 3E$
3. $0, 2E, 3E, 5E$
4. $0, 5E, 8E, 10E$

The Lyman series of photons each have an energy capable of exciting the electron of a hydrogen atom from the ground state (energy level 1) to energy levels 2, 3, 4, etc. The wavelengths of the first five photons in this series are 121.6 nm, 102.6 nm, 97.3 nm, 95.0 nm, and 93.8 nm. The ground state energy of hydrogen is −13.6 eV. Based on the wavelengths of the Lyman series, calculate the energies of the first five excited states above ground level for a hydrogen atom to the nearest 0.1 eV.

The ground state of a certain type of atom has energy $–E_o$. What is the wavelength of a photon with enough energy to ionize an atom in the ground state and give the ejected electron a kinetic energy of $2E_o$?

1. $\dfrac{hc}{3E_o}$
2. $\dfrac{hc}{2E_o}$
3. $\dfrac{hc}{E_o}$
4. $\dfrac{2hc}{E_o}$

An electron in a hydrogen atom is initially in energy level 2 ($E_2 = -3.4\textrm{ eV}$). (a) What frequency of photon must be absorbed by the atom in order for the electron to transition to energy level 3 ($E_3 = -1.5\textrm{ eV}$)? (b) What frequency of photon must be emitted by the atom in order for the electron to transition to energy level 1 ($E_1 = -13.6\textrm{ eV}$)?

A sample of hydrogen gas confined to a tube is initially at room temperature. As the gas is heated, the observer notices that the gas begins to glow with a pale pink color. Careful study of the spectrum shows that the light spectrum is not continuous. Instead, the hydrogen gas is only emitting visible wavelength photons of four specific colors, which combine to form the overall color to the human eye. What is the best way to explain this behavior?

1. As the gas heats up, atoms have more and more collisions and close approaches, so frictional heating causes the gas to glow.
2. As the gas heats up, the electrons within the hydrogen atoms are excited to high energy levels. As the electrons transition to lower energies, they emit light of specific colors.
3. As the gas heats up, more and more collisions occur, and the energy lost in these inelastic collisions is converted into light.
4. As the gas heats up, the turbulence of the gas within the tube causes friction between the gas and the walls of the container, causing the gas to glow.

A rock is illuminated with high energy ultraviolet light. This causes the rock to emit visible light. Explain what is happening in the atomic substructure of the rock that causes this effect, which we call fluorescence.

Which of the following is the best way of explaining why the leaves on a given tree are green?

1. The molecules in the leaves absorb all visible light but strongly reflect green light.
2. The molecules in the leaves absorb green light and reflect other visible light.
3. The molecules are excited by external light sources, and their electrons emit green light when they are de-excited to a lower energy level within the molecules.
4. The molecules glow with a characteristic green energy in order to balance the absorption of energy due to light and heat from their surroundings.

Explain what phosphorescence is and how it differs from fluorescence. Which process typically takes longer and why?

An electron is excited from the ground state of an atom (energy level 1) into a highly excited state (energy level 8). Which of the following electron behaviors represents the fluorescence effect by the atom?

1. The electron remains at level 8 for a very long time, then transitions up to level 9.
2. The electron transitions directly down from level 8 to level 1.
3. The electron transitions from level 8 to level 1 and then returns quickly to level 8.
4. The electron transitions from level 8 to level 6, then to level 5, then to level 3, then to level 1.

Describe the process of fluorescence in terms of the emission of photons as electron transitions between energy states. Specifically, explain how this process differs from ordinary atomic emission.

Figure 30.66 This figure shows graphical representations of the wave functions of two particles, X and Y, that are moving in the positive x-direction. The maximum amplitude of particle X’s wave function is $A_0$. Which particle has a greater probability of being located at position $x_o$ at this instant, and why?

1. Particle X, because the wave function of particle X spends more time passing through $x_o$ than the wave function of particle Y.
2. Particle X, because the wave function of particle X has a longer wavelength than the wave function of particle Y.
3. Particle Y, because the wave function of particle Y is narrower than the wave function of particle X.
4. Particle Y, because the wave function of particle Y has a greater amplitude near $x_o$ than the wave function of particle X.

In Figure 30.66, explain qualitatively the difference in the wave functions of particle X and particle Y. Which particle is more likely to be found at a larger distance from the coordinate x0 and why? Which particle is more likely be found exactly at x0 and why?

For an electron with a de Broglie wavelength $\lambda$, which of the following orbital circumferences within the atom would be disallowed? Select two answers.

1. $0.5\lambda$
2. $\lambda$
3. $1.5\lambda$
4. $2\lambda$

We have discovered that an electron’s orbit must contain an integer number of de Broglie wavelengths. Explain why, under ordinary conditions, this makes it impossible for electrons to spiral in to merge with the positively charged nucleus.