Question
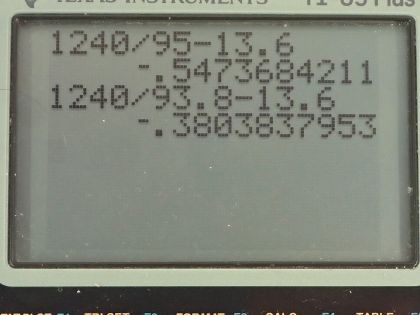
The Lyman series of photons each have an energy capable of exciting the electron of a hydrogen atom from the ground state (energy level 1) to energy levels 2, 3, 4, etc. The wavelengths of the first five photons in this series are 121.6 nm, 102.6 nm, 97.3 nm, 95.0 nm, and 93.8 nm. The ground state energy of hydrogen is −13.6 eV. Based on the wavelengths of the Lyman series, calculate the energies of the first five excited states above ground level for a hydrogen atom to the nearest 0.1 eV.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 4 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A photon hitting a ground state electron for hydrogen can excite it to the second principal quantum number— this second shell— if the photon has just the right amount of energy equal to the difference between these energy levels— n equals 2 and n equals 1— and that energy of the photon has to be E 2 minus E 1 where E 1 we are given— it's the ground state energy, which is negative 13.6 electron volts— and we know that we are dealing with n equals 1 as our initial state because we are told that these photons are from the Lyman series and for the Lyman series... well when the electron is emitting a photon, the Lyman series has the final state equal to 1 but I guess in this case, it's the initial state that's 1 because we are talking about a photon being incident and causing the electron to transition up to the excited state. Okay! So the wavelength that causes an excitation to level 2 starting at level 1 is 121.6 nanometers and a different photon that goes all the way to level 3 starting at level 1 will have a wavelength of 102.6 nanometers and then so on and so on up to levels 4, 5 and 6 all starting at level 1 and so these wavelengths are in order of increasing energy so energy is going up as you go down this list here; as the wavelengths gets shorter, the energy increases. The energy of the photon is given by this formula Planck's constant times speed of light divided by wavelength and so as this denominator reduces, the quotient increases and this energy of this photon is the difference in the energy of the electron at these two different levels and so we want to figure out what is the energy of the electron at n equals 2? So energy at 2 minus energy at 1 is the photon energy and then we'll add energy at level 1 to both sides and we have E 2 then is hc over λ 21 plus E 1. So that's 1240 electron volt nanometers, which is a convenient way of writing h times c with units that will cancel in the numerator and denominator if you write the denominator in nanometers and it will leave us with electron volts in the top here. So we have 1240 electron volt nanometers divided by 121.6 nanometers, plus negative 13.6 electron volts for the ground state energy and that is negative 3.4 electron volts is the energy at n equals 2. At energy at n equals 3, it's going to be the same formula but we're just using the wavelength that was needed to excite the electron from the ground state to n equals 3. So it's 1240 divided by 102.6 plus negative 13.6 and that is negative 1.5 electron volts and then so on and so on it's the same each formula each time but plugging in different wavelengths. So for energy state 4, we are plugging in 97.3 nanometers getting an energy of negative 0.8 electron volts; for energy level 5, we have 95.0 nanometers and that's negative 0.5 electron volts for that energy and energy level 6, we are plugging in wavelength of 93.8 nanometers giving us an energy of negative 0.4 electron volts.