Question
(a) What voltage must be applied to an X-ray tube to obtain 0.0100-fm-wavelength X-rays for use in exploring the details of nuclei? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- Electrodes would need to be 41 km apart to avoid sparks through air. This voltage is unreasonably high.
- The wavelength is too short.
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 68 (Problems & Exercises)
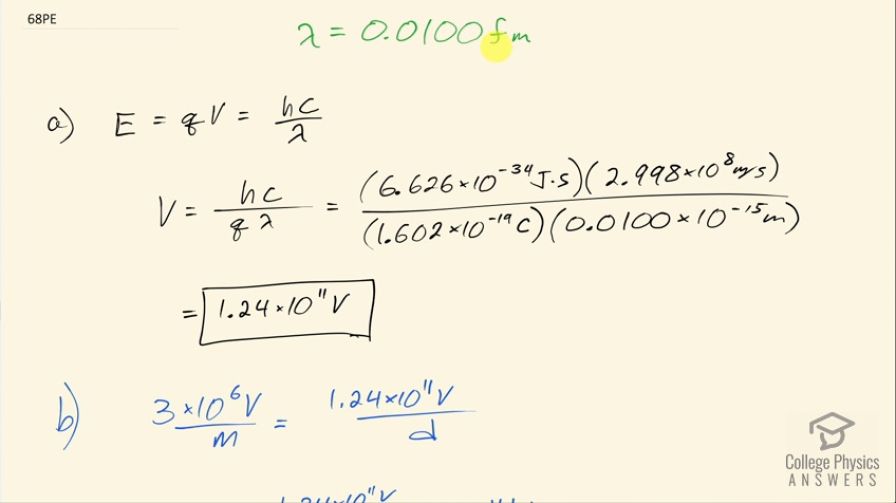
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
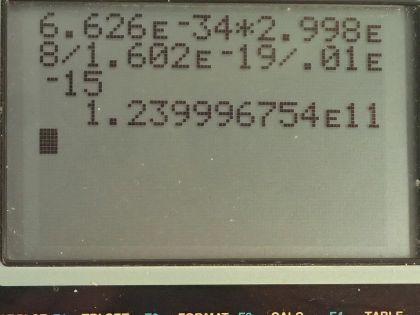
This is College Physics Answers with Shaun Dychko. An x-ray with a wavelength of 0.0100 femtometers is meant to be produced by accelerating electrons in a x-ray tube. So the energy of these electrons if they convert all of their kinetic energy into photon energy will have a energy of the charge times the voltage through which they are accelerated and that has to equal the energy of the photon that it produces, which is Planck's constant times speed of light divided by wavelength and we can solve for V by dividing both sides by q and we end up with the voltage then is Planck's constant times speed of light divided by the charge of an electron times the wavelength. So that's 6.626 times 10 to the minus 34 joule seconds times speed of light divided by elementary charge times 0.0100 times 10 to the minus 15 meters and that is 1.24 times 10 to the 11 volts. That voltage is way too high and to illustrate kind of why, let's consider what the dielectric strength is of air and it has a dielectric breakdown at 3 megavolts per meter so that means given a voltage of 3 megavolts, there would be a spark that would occur through air over a distance of 1 meter or less. Okay! So that dielectric strength is going to equal this voltage that we calculated divided by the separation you would need between electrodes that have this voltage difference between them to not have a spark. So we'll solve for d here by multiplying both sides by d over 3 times 10 to the 6 and you have the separation you would need between electrodes then is 1.24 times 10 to the 11 volts divided by 3 megavolts per meter and that's 41 kilometers. That's impractical... you could get around this I guess by having the apparatus in a vacuum but then that becomes its own set of problems to maintain a vacuum around everything so this voltage is unreasonably high and the wavelength is too short, it's unreasonable to expect a 0.0100 femtometer x-ray to be created with this method.