Question
(a) An excimer laser used for vision correction emits 193-nm UV. Calculate the photon energy in eV.
(b) These photons are used to evaporate corneal tissue, which is very similar to water in its properties. Calculate the amount of energy needed per molecule of water to make the phase change from liquid to gas. That is, divide the heat of vaporization in kJ/kg by the number of water molecules in a kilogram.
(c) Convert this to eV and compare to the photon energy. Discuss the implications.
Final Answer
- . Each photon can vaporize approximately 15 water molecules.
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 64 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
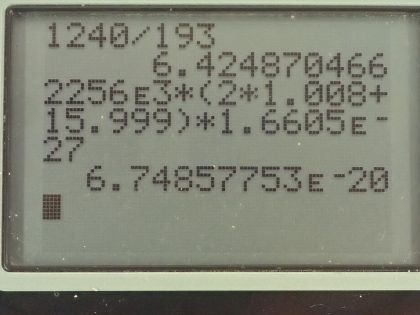
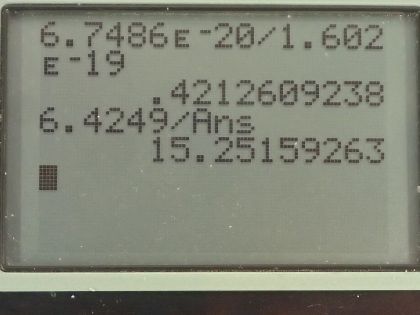
This is College Physics Answers with Shaun Dychko. An excimer laser that's used for eye surgery so that people don't need glasses anymore emits a wavelength of 193 nanometers and the question is what's the energy of one of these photons? Well that will be Planck's constant times speed of light divided by the wavelength and we can write hc as 1240 electron volt nanometers if we have the denominator also in units of nanometers those nanometers will cancel and we'll be left with an answer in electron volts. So we have 1240 divided by 193 and that's 6.42 electron volts per photon. In part (b), we are asked how much energy is needed to vaporize a single molecule of water, which is H 2 O? So we take the latent heat of vaporization, which is in table [14.2] so latent heat of vaporization for water is 2256 times 10 to the 3 joules per kilogram but we want to figure out what is this in joules per molecule? So we need to figure out how many kilograms there are per molecule of water? So the first thing we can do is figure out how many atomic mass units there are in a single molecule and we can use appendix A to help for figuring that out. So a hydrogen atom has an atomic mass of 1.008 atomic mass units and the other isotopes are really rare so we'll just take this number directly—1.008— and then we'll multiply that by 2 because there are two hydrogen atoms in every water molecule and then add to that the atomic mass of oxygen, which 99.76 percent of it is this isotope so we'll take this atomic mass here— 15.995 atomic mass units... I guess this is a 5 here actually but I don't think it will change the answer. Okay! So add those terms together in the numerator there and then multiply it by the number of kilograms there are for every atomic mass unit— that's 1.6605 times 10 to the minus 27 kilograms per atomic mass unit— this works out to 6.75 times 10 to the minus 20 joules per water molecule. If we convert this into electron volts, we multiply that by 1 electron volt for every 1.602 times 10 to the minus 19 joules and that 0.421 electron volts are needed to vaporize each molecule of water. If we take the energy in a single photon— 6.4249 electron volts— and divide it by the energy needed to vaporize each molecule, we get 15.3 and this is in units of molecules because if you multiply top and bottom by molecule units, you will see that it cancels on the bottom and we are left with molecules on the top after the electron volts cancel. This is to say that each photon can vaporize about 15 water molecules.