Question
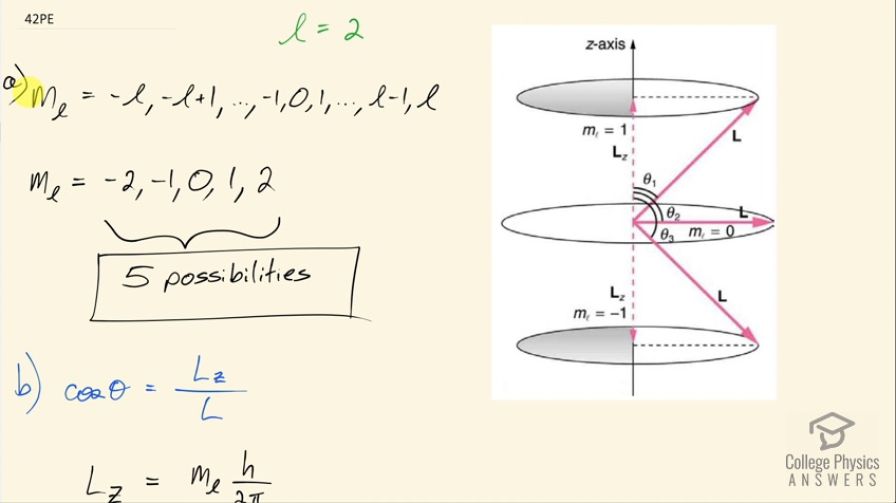
(a) How many angles can make with the z -axis for an electron? (b) Calculate the value of the smallest angle.
Final Answer
- 5 possibilities
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 42 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
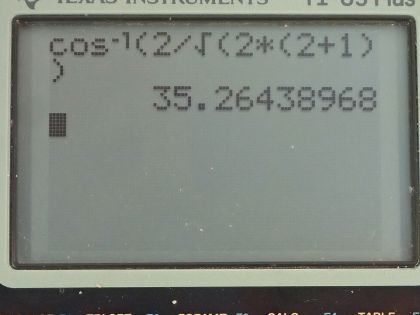
This is College Physics Answers with Shaun Dychko. The angular momentum quantum number for an electron is 2 and question (a) asks us how many possible angles can the angular momentum vector make with the z-axis? So here's a picture depicting some different positions for the angular momentum vector and in a dotted pink line, we have l subscript z, which is the component of the angular momentum along the z-axis or with different words, we could call this the projection of the angular momentum vector on the z-axis and each different length of this projection corresponds to a different value of this quantum number, which is the angular momentum projection quantum number—m l— so really the question is asking how many different values for m l are possible given l equal to 2? So this is the sequence that describes all the possible values for m l in terms of l so it starts at negative l and goes in integers up to l. So for l equal to 2, it can be at a minimum negative 2, or negative 1 or 0 or 1 or 2 so there are five possibilities in this list of possibilities for the angular momentum projection quantum number. Part (b) asks for the smallest possible angle between the angular momentum vector and the z-axis. So the angle is measured between the z-axis and the vector and so cosine of this angle then is going to be this adjacent leg, which is the projection of the angular momentum on the z-axis divided by the hypotenuse, which is the magnitude of the angular momentum and this is a right triangle here and so cos Θ is L z over L in other words; L z we are told is the angular momentum projection number times Planck's constant over 2π whereas L—capital L I should say— is the square root of the angular momentum quantum number times l plus 1 and then multiply all that by Planck's constant over 2π and so we can substitute each of these in our formula for cos of this angle. So cos of the angle between the z-axis and the angular momentum is m l times h over 2π divided by square root l times l plus 1 over h over 2π, these fractions cancel and we are left with this formula here. Now we want to minimize the angle so the thing we can adjust in this formula is this number here m l; l we are told is 2—that's fixed— but we can choose which value of m l here and we have to choose a value such that we minimize Θ. This is a graph of y equals cos Θ and it has a maximum of 1 at an angle of 0 and so the closer we get to this maximum for cos Θ, the closer we get to this minimum value of Θ... the closer we get to Θ equal to 0. So we want to maximize cos Θ in other words and doing so will minimize Θ. So the maximum cos Θ then will occur when we maximize the numerator here so we take the largest possible value for the angular momentum projection number. Now Θ is the inverse cos of all this so that's what I have written here so we are taking the inverse cos of the maximum value of m l, which is 2 and dividing that by the square root of 2 times 2 plus 1 and this works out to 35.3 degrees.