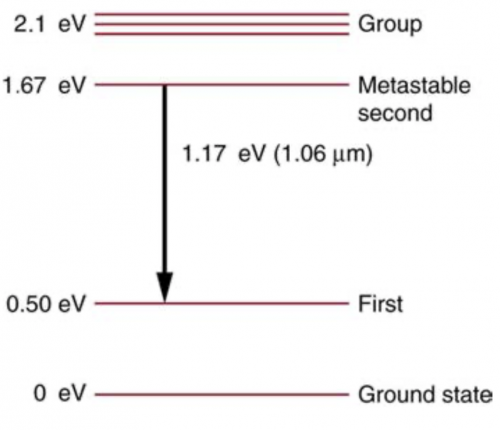
Some of the most powerful lasers are based on the energy levels of neodymium in solids, such as glass, as shown in Figure 30.65. (a) What average wavelength light can pump the neodymium into the levels above its metastable state? (b) Verify that the 1.17 eV transition produces $1.06\mu \text{m}$ radiation.

Video Transcript

This is College Physics Answers with Shaun Dychko. This is an energy level diagram for neodymium and question (a) is asking what wavelength of light would be needed to stimulate an electron from the ground state up into this group that's above the metastable state? So this difference in energy is 2.1 electron volts. So we'll use this formula which says the energy of a photon is Planck's constant times speed of light divided by the wavelength and we will multiply both sides by λ over energy to solve for the wavelength needed and hc is 1240 electron volt nanometers and we will divide that by the energy of the photon, which is 2.1 electron volts and that will work out to 590 nanometers. So a photon that's incident with this wavelength— 590 nanometers— is capable of stimulating an electron from the ground state up into this group up here because all the photon energy will be absorbed by the electron and thereby increase the electron's energy. Okay! Part (b) says verify that the transition from the metastable second state to the first state results in a photon with a wavelength of 1.06 micrometers. So we'll use the same formula for the wavelength so that's 1240 electron volt nanometers divided by 1.17 electron volts and that is 1059.8 nanometers which we then convert into micrometers and sure enough, it's 1.06 micrometers.