Question
What angles can the spin of an electron make with the z -axis?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 43 (Problems & Exercises)
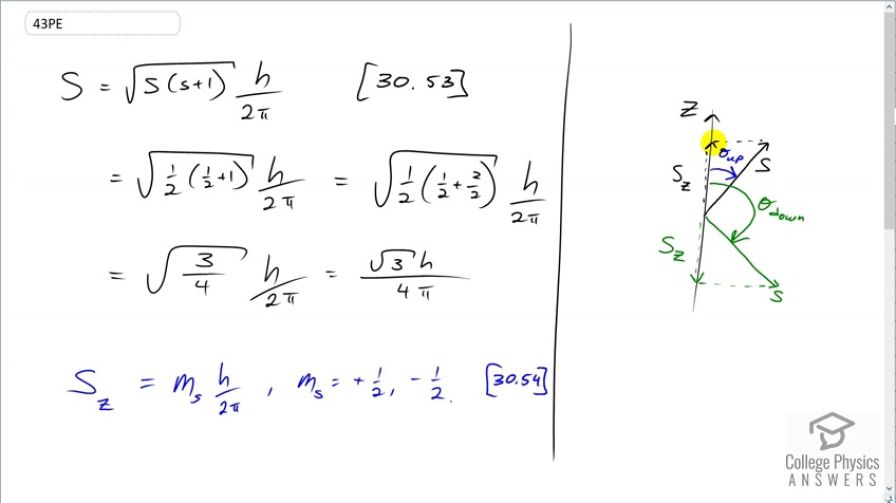
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Electrons have a spin angular momentum which is a vector and that vector will have a component that's along some z-axis that you can choose and we have formulas for the size of this component; this is the Z-component of the angular spin and that's the angular spin projection quantum number times h over 2π. And then we have the spin angular momentum which is square root times the spin quantum number times s plus 1 again, all square rooted times h over 2π; this s though is always one-half when you are talking about electrons. And so this formula can be rewritten as root 3h over 4π when you are talking about electrons because we have square root one-half times a half plus 1 and one half plus 1 is 3 over 2 and then multiplied by a half is 3 over 4 and then square root of 3 over 4 is square root 3 over 2 and then the 2 in this denominator times the 2 in this denominator makes a 4 that's there. So this spin angular momentum then for an electron is root 3h over 4π. Now the component of that vector along the z-axis is given by this formula and the question here is to figure out what is this angle between this Z-component and the hypotenuse? So it becomes a vector question and we are gonna use inverse cosine to answer that question because this angle is between the adjacent and the hypotenuse. So we need the inverse cosine of the adjacent divided by the hypotenuse because cos Θ is the adjacent divided by hypotenuse and so Θ then is the inverse cosine of that ratio. So for the angle when you have the spin projection quantum number is positive a half because it can be either positive a half or the spin projection quantum number can be negative a half as well; when it's positive a half, it's gonna be also called up and it's gonna be this angle and so that's inverse cosine of substituting for each of these things we are gonna have positive a half for m s times h over 2π—that's a substitution for S Z— and then multiplying it by the reciprocal of this spin angular momentum. So dividing by this fraction is the same as multiplying by its reciprocal so I'm multiplying by 4π over root 3h and the h's cancel and so do the π's and the 4 reduces to 2 which then multiplies by half to make 1 in the numerator and a root 3 in the denominator. So it's the inverse cosine of 1 over root 3 which is 54.7 degrees. So this angle here is 54.7 degrees. And then to this other other scenario, when you have spin down or the spin projection quantum number is negative a half, we are gonna get this answer in green. And so we have negative a half here whereas we had positive a half before and so we are gonna get negative 1 over root 3 inverse cosine and that makes 125 degrees. And so with respect to the vertical positive axis, this is going to be 125 degrees between the z-axis and the spin angular momentum when the projection quantum number is negative a half.
